Let ((X, d)) be a locally compact metric space and (mu, mu_{n} in mathfrak{M}_{mathrm{r}}^{+}(X), mu_{n} stackrel{mathrm{v}}{ightarrow} mu).
Question:
Let \((X, d)\) be a locally compact metric space and \(\mu, \mu_{n} \in \mathfrak{M}_{\mathrm{r}}^{+}(X), \mu_{n} \stackrel{\mathrm{v}}{ightarrow} \mu\). Prove that
\[\lim _{n} \int_{B} u d \mu_{n}=\int_{B} u d \mu \quad \forall u \in C_{c}(X), B \in \mathscr{B}(X), \mu(\partial B)=0\]
[ have a look at the proof of Theorem 21.15 (iii).]
Data from theorem 21.15(iii)
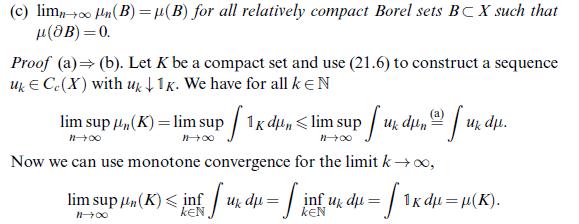
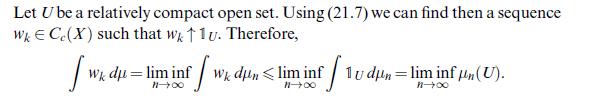
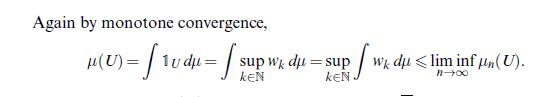
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





