Let \((X, \mathscr{A}, \mu)\) be a measure space and let \(\mathscr{G} \subset \mathscr{A}\) be a sub- \(\sigma\)-algebra such that \(\left.\muight|_{\mathscr{G}}\) is \(\sigma\)-finite. Let \(p, q \in(1, \infty)\) be conjugate numbers, i.e. \(1 / p+1 / q=1\), and let \(u, w \in\) \(\bigcap_{p \in[1, \infty]} L^{p}(\mathscr{A}, \mu)\). Show that

\[\left|\mathbb{E}^{\mathscr{G}}(u w)ight| \leqslant\left[\mathbb{E}^{\mathscr{G}}\left(|u|^{p}ight)ight]^{1 / p}\left[\mathbb{E}^{\mathscr{G}}\left(|w|^{q}ight)ight]^{1 / q} .\]

[ use Lemma 13.1 with \(A=|u| /\left[\mathbb{E}^{\mathscr{G}}\left(|u|^{p}ight)ight]^{1 / p}\) and \(B=|w| /\left[\mathbb{E}^{\mathscr{C}}\left(|w|^{q}ight)ight]^{1 / q}\) whenever the numerator is not 0 .]

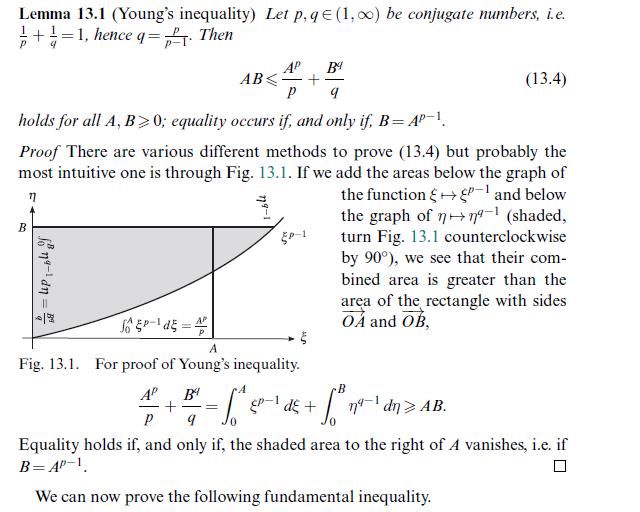
Data from lemma 13.1

Transcribed Image Text:

Lemma 13.1 (Young's inequality) Let p, q= (1, 0) be conjugate numbers, i.e. +1=1, hence q=. Then B fon-dn= P 9 holds for all A, B>0; equality occurs if, and only if, B=AP-1. Proof There are various different methods to prove (13.4) but probably the most intuitive one is through Fig. 13.1. If we add the areas below the graph of the function +-1 and below the graph of n+n9- (shaded, turn Fig. 13.1 counterclockwise by 90), we see that their com- bined area is greater than the area of the rectangle with sides OA and OB, EP-dE= = AP B + AB < + A Fig. 13.1. For proof of Young's inequality. -- 5P-1 = -1 de + P 9 B9 B 66 m - dn> AB. (13.4) 779-1 Equality holds if, and only if, the shaded area to the right of A vanishes, i.e. if B = AP-1 We can now prove the following fundamental inequality.