Show that for every parameter > 0 > 0 the function x ( sin x x ) 3 e x

Show that for every parameter $\alpha >0$ the function

$$x\mapsto {\left(\frac{\sin x}{x}\right)}^3{e}^{-\alpha x}$$

is integrable over $(0,\infty )$ and that the integral is continuous as a function of the parameter. [ find piecewise integrable majorants like in Problem 12.18 ; use the continuity lemma.]

Data from problem 12.8

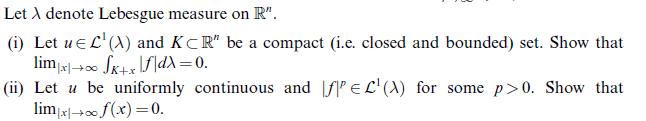
Let A denote Lebesgue measure on R". (i) Let u L (A) and KCR" be a compact (i.e. closed and bounded) set. Show that limx SK+x|f|dx=0. (ii) Let u be uniformly continuous and fPEL(A) for some p>0. Show that limx f(x) = 0.