Show that the outer regularity from Corollary 18.10 coincides with the usual notion, i.e. [overline{mathcal{H}}^{phi}(A)=inf left{mathcal{H}^{phi}(U): U
Question:
Show that the outer regularity from Corollary 18.10 coincides with the usual notion, i.e.
\[\overline{\mathcal{H}}^{\phi}(A)=\inf \left\{\mathcal{H}^{\phi}(U): U \supset A, U \text { open }ight\},\]
provided that there exists some open set \(U \supset A\) with finite Hausdorff measure. Use the example \(\mathcal{H}^{0}\) (counting measure) to show that this condition is essential.
Data from corollary 18.10
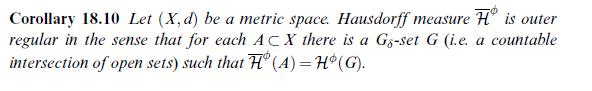

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





