The differentiability lemma revisited. Let ((X, mathscr{A}, mu)) be a (sigma)-finite measure space and (phi) : (mathbb{R}
Question:
The differentiability lemma revisited. Let \((X, \mathscr{A}, \mu)\) be a \(\sigma\)-finite measure space and \(\phi\) : \(\mathbb{R} \times X ightarrow \mathbb{R}\) a mapping with the following properties.
(i) \(\int_{X}|\phi(t, x)| \mu(d x)
(ii) \(t \mapsto \phi(t, x)\) is differentiable for all \(x \in X, \int_{X}\left|\partial_{t} \phi(t, x)ight| \mu(d x)
\[\int_{K} \int_{X}\left|\partial_{t} \phi(t, x)ight| \mu(d x) d t
for any compact set \(K \subset \mathbb{R}\)
(iii) \(t \mapsto \int_{X} \partial_{t} \phi(t, x) \mu(d x)\) is continuous.
Then show that \(F(t):=\int_{X} \phi(t, x) \mu(d x)\) is continuously differentiable for all \(t \in \mathbb{R}\) and
\[F^{\prime}(t)=\int_{X} \partial_{t} \phi(t, x) \mu(d x), \quad t \in \mathbb{R}\]
Remark. I owe this variant of Theorem 12.5 to Franziska Kühn. The paper by Talvila [55] contains further versions of this theorem.
Data from theorem 12.5
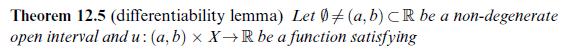
a. 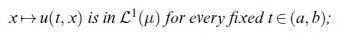
b. 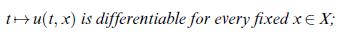
c. 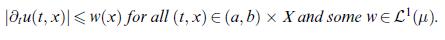



Step by Step Answer:






