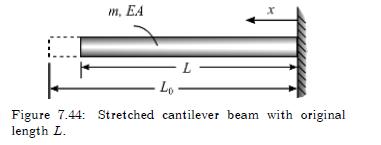
A cantilever beam has its free end stretched uniformly so that the original length \(L\) becomes \(L_{0}\), and then it is released at \(t=0\), as shown in Figure 7.44. Begin with the general solution for the axial response of a beam,

\[ \begin{aligned} u(x, t)= & \sum_{r=1}^{\infty} \sin \frac{(2 r-1) \pi x}{2 L} \\ \times & \left(A_{r} \sin \frac{(2 r-1) \pi x}{2 L} \sqrt{\frac{E A}{m}} t\right. \\ & \left.+B_{r} \cos \frac{(2 r-1) \pi x}{2 L} \sqrt{\frac{E A}{m}} t\right) \end{aligned} \]

then satisfy the boundary conditions to fix the arbitrary constants, and finally derive the particular response.

Transcribed Image Text:

m. EA x Lo Figure 7.44: Stretched cantilever beam with original length L.