Derive the equation of motion and natural frequency for a disk in motion that is constrained to
Question:
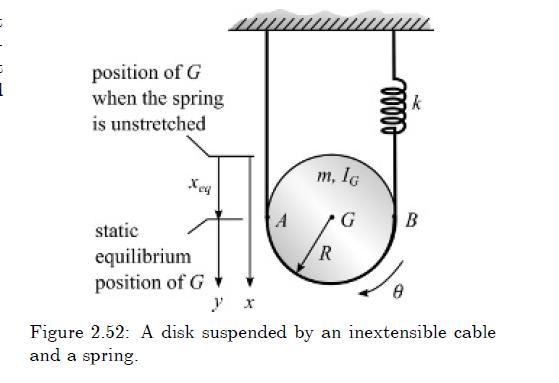
Derive the equation of motion and natural frequency for a disk in motion that is constrained to move vertically, but can rotate, as shown in Figure 2.52. The coordinate \(y\) is the displacement of its center of mass, measured from the static equilibrium position, and the coordinate \(x\) is the displacement of the center of mass measured from its location when the spring is unstretched. Let \(\theta\) be the rotation of the disk measured from the static equilibrium position.
The mass of the disk is \(m\), and the mass moment of inertia for the disk is \(m R^{2} / 2\). Assume that the cable is inextensible and the spring constant is \(k\).
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Mechanical Vibration Analysis, Uncertainties, And Control
ISBN: 9781498753012
4th Edition
Authors: Haym Benaroya, Mark L Nagurka, Seon Mi Han
Question Posted:





