For Example 4.16 derive the equation of motion using \(x\) as the generalized coordinate. Then solve this equation with initial conditions \(x_{0}, v_{0}\) to find

\[ x(t)=\frac{v_{0}}{\omega} \sin \omega t-\frac{m g}{2 k} \sin \phi(\cos \omega t-1)+x_{0} \]

where \(\omega=\sqrt{4 k / 3 m}\).

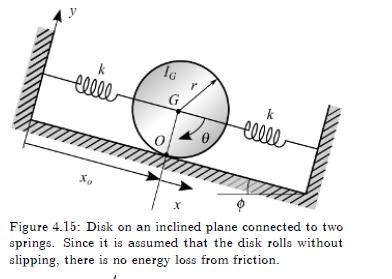
Example 4.16 A Rolling Disk The disk on the inclined plane of Figure 4.15 is supported by two massless springs. It rolls without slipping, and thus there is no dissipation of energy. The disk oscillates about the static equilibrium position to indefinitely, and at the equilibrium position has a velocity of vo. Use La- grange's equation to derive the equation of motion for arbitrary initial displacement and velocity.