In Problem 40, solve for the response where the system damping is

(a) \([C]=2[M]\),

(b) \([C]=3[K]\),

(c) \([C]=2[M]+3[K]\). 

In each discuss the results, especially regarding how the damping for each mode depends on the proportional damping model. Let \(\sqrt{k / m}\) be \(1 \mathrm{rad} / \mathrm{s}\) if necessary.

Problem 40:

Solve Example 6.14 with the equation of motion

\[ \begin{gathered} {\left[\begin{array}{cc} m & 0 \\ 0 & m \end{array}\right]\left\{\begin{array}{c} \ddot{x}_{1} \\ \ddot{x}_{2} \end{array}\right\}+\left[\begin{array}{cc} 3 k & -2 k \\ -2 k & 2 k \end{array}\right]\left\{\begin{array}{l} x_{1} \\ x_{2} \end{array}\right\}} \\ =\left\{\begin{array}{c} F_{1}(t) \\ F_{2}(t) \end{array}\right\} \end{gathered} \]

for \(F_{1}(t)=\cos (0.66 \sqrt{k / m} t)\) and \(F_{2}(t)=0\). Plot the displacement time histories.

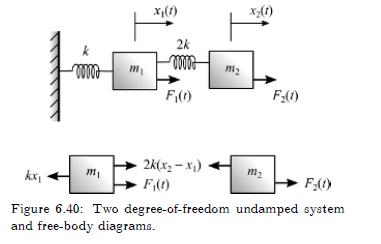
Example 6.14 Forced Vibration Modal Analysis Using modal analysis solve for the displacements in the two degree-of-freedom system without damping, shown in Figure 6.40.