Repeat Problem 15 for the transfer function

\[ T(s)=\frac{K s^{2}}{K s^{2}+s+1} \]

Problem 15:

A system transfer function is given by

\[ T(s)=\frac{K s}{K s^{2}+1} \]

Derive the sensitivity function and determine the value(s) of \(K\) that minimize sensitivity. Plot \(T(s)\) for \(K=1,10,100\) on one set of axes and draw conclusions from the comparison. Plot the sensitivity function for each of the \(K\) values, also on one set of axes. Which value of \(K\) reduces sensitivity?


Figure 10.31: Mechanical system with two masses, two dampers, and one spring acted on by an external force.

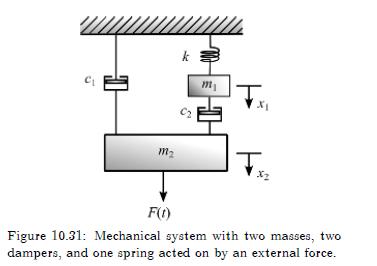
k m F(t) Figure 10.31: Mechanical system with two masses, two dampers, and one spring acted on by an external force.