Solve Problem 4.95 using MATLAB program ode23 if the system is viscously damped so that the equation of motion is\[2 \ddot{x}+10 \dot{x}+1500 x=F(t)\]

Data From Problem 4.95:-

The equation of motion of an undamped system is given by \(2 \ddot{x}+1500 x=F(t)\), where the forcing function is defined by the curve shown in Fig. 4.73. Find the response of the system numerically for \(0 \leq t \leq 0.5\). Assume the initial conditions as \(x_{0}=\dot{x}_{0}=0\) and the step size as \(\Delta t=0.01\). Use the MATLAB program ode23.

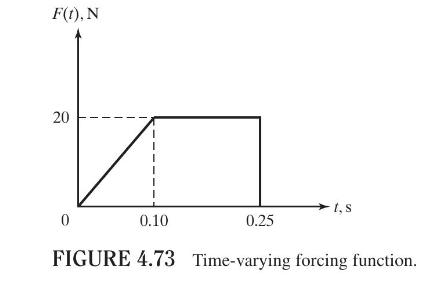
F(t), N 20 0 0.10 0.25 FIGURE 4.73 Time-varying forcing function.