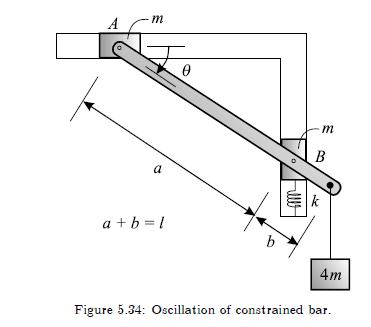
The lightweight bar in Figure 5.34 is released from rest when the spring is undeformed at \(\theta=0\). The two masses at \(A\) and \(B\) slide in frictionless guides that are horizontal at the left and vertical at the right. Formulate the equation of motion using

(a) Newton's second law,

(b) Lagrange's equation, and

(c) Hamilton's principle.

Assume the bar is massless. Show that the equation of motion is

\[
\begin{aligned}
& \left(a^{2}+4 l^{2} \cos ^{2} \theta+4 b^{2} \sin ^{2} \theta\right) \ddot{\theta} \\
& +2\left(b^{2}-l^{2}\right) \dot{\theta}^{2} \sin 2 \theta \\
& +g(5 a+4 b) \cos \theta+\frac{1}{2} \frac{k}{m} a^{2} \sin 2 \theta=0
\end{aligned}
\]

Transcribed Image Text:

A m a m B k a+b=l b 4m Figure 5.34: Oscillation of constrained bar.