Write a computer program for finding the steady-state response of a two-degree-of-freedom system under the harmonic excitation \(F_{j}(t)=F_{j 0} e^{i \omega t}\) and \(j=1,2\) using Eqs. (5.29) and (5.35). Use this program to find the response of a system with \(m_{11}=m_{22}=2.5 \mathrm{~kg}, m_{12}=0\), \(c_{11}=250 \mathrm{~N}-\mathrm{s} / \mathrm{m}, c_{12}=c_{22}=0, k_{11}=8000 \mathrm{~N} / \mathrm{m}, k_{22}=4000 \mathrm{~N} / \mathrm{m}, k_{12}=-4000 \mathrm{~N} / \mathrm{m}\), \(F_{10}=5 \mathrm{~N}, F_{20}=10 \mathrm{~N}\), and \(\omega=5 \mathrm{rad} / \mathrm{s}\).

Equation 5.29 and 5.35:-

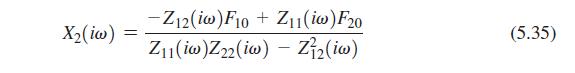
x;(t) = Xjeiwt j = 1,2 (5.29)