(a) Show that, for bosons as well as fermions, [ left[psileft(boldsymbol{r}_{j}ight), hat{H}ight]=left(-frac{hbar^{2}}{2 m} abla_{j}^{2}+int d^{3} r psi^{dagger}(boldsymbol{r})...
Question:
(a) Show that, for bosons as well as fermions,
\[ \left[\psi\left(\boldsymbol{r}_{j}ight), \hat{H}ight]=\left(-\frac{\hbar^{2}}{2 m} abla_{j}^{2}+\int d^{3} r \psi^{\dagger}(\boldsymbol{r}) u\left(\boldsymbol{r}, \boldsymbol{r}_{j}ight) \psi(\boldsymbol{r})ight) \psi\left(\boldsymbol{r}_{j}ight) \]
where \(\hat{H}\) is the Hamiltonian operator defined by equation (11.1.4).
Data From Equation (11.1.4)
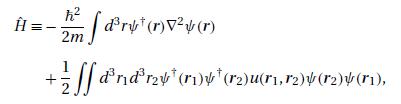
(b) Making use of the foregoing result, show that the equation \[
\begin{aligned}
\frac{1}{\sqrt{ } N !}\left\langle 0\left|\psi\left(\boldsymbol{r}_{1}ight) \ldots \psi\left(\boldsymbol{r}_{N}ight) \hat{H}ight| \Psi_{N E}ightangle & =E \frac{1}{\sqrt{ } N !}\left\langle 0\left|\psi\left(\boldsymbol{r}_{1}ight) \ldots \psi\left(\boldsymbol{r}_{N}ight)ight| \Psi_{N E}ightangle \\
& =E \Psi_{N E}\left(\boldsymbol{r}_{1}, \ldots \boldsymbol{r}_{N}ight)
\end{aligned}
\]
is equivalent to the Schrödinger equation (11.1.15).
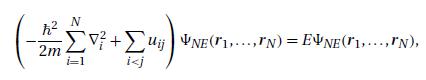
Step by Step Answer:






