Consider the linearized RG transformation (14.3.12), with
\[
\mathfrak{A}_{l}^{*}=\left(\begin{array}{ll}
a_{11} & a_{12}  \tag{3}\\
a_{21} & a_{22}
\end{array}\right)
\]
such that \(\left(a_{11} a_{22}-a_{12} a_{21}\right) eq 0\). We now introduce the "generalized coordinates" \(u_{1}\) and \(u_{2}\) through equations (14.3.13); clearly, \(u_{1}\) and \(u_{2}\) are certain linear combinations of the system parameters \(k_{1}\) and \(k_{2}\).
(a) Show that the slopes of the lines \(u_{1}=0\) and \(u_{2}=0\), in the \(\left(k_{1}, k_{2}\right)\)-plane, are
\[
m_{1}=\frac{a_{21}}{\lambda_{2}-a_{22}}=\frac{\lambda_{2}-a_{11}}{a_{12}} \quad \text { and } \quad m_{2}=\frac{a_{21}}{\lambda_{1}-a_{22}}=\frac{\lambda_{1}-a_{11}}{a_{12}}
\]
respectively; here, \(\lambda_{1}\) and \(\lambda_{2}\) are the eigenvalues of the matrix \(\mathcal{A}_{l}^{*}\). Verify that the product \(m_{1} m_{2}=-a_{21} / a_{12}\) and hence the two lines are mutually perpendicular if and only if \(a_{12}=a_{21}\).
(b) Check that, in the special case when \(a_{12}=0\) but \(a_{21} eq 0\), the above slopes assume the simple form
\[
m_{1}=\infty \quad \text { and } \quad m_{2}=a_{21} /\left(a_{11}-a_{22}\right)
\]
whereas, in the special case when \(a_{21}=0\) but \(a_{12} eq 0\), they become
\[
m_{1}=\left(a_{22}-a_{11}\right) / a_{12} \quad \text { and } \quad m_{2}=0 \text {; }
\]
note that Figure 14.7 pertains to the latter case.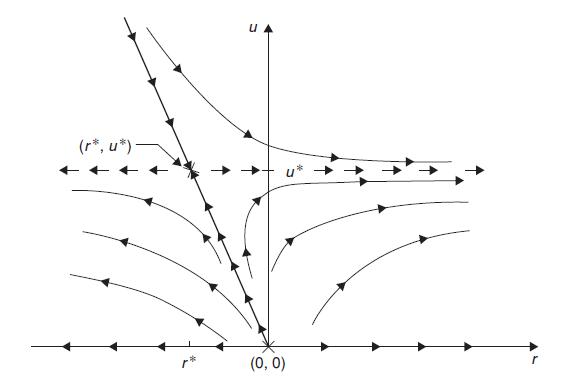

(c) Examine as well the cases for which either \(a_{11}\) or \(a_{22}\) is zero; Figure 14.6 pertains to the latter of these cases.

Transcribed Image Text:

+ (r, u*)- (0, 0)