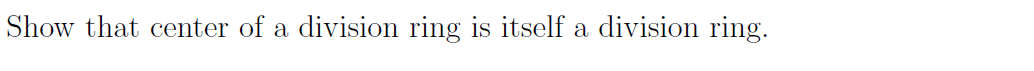
\fLet R be a commutative ring with identity and G be a finite group such that G = {91, 92, ..., 9n}. Consider the =n R[G] = (a = > aigi : di E R}. i=1 Then R[G] is a ring with respect to the following operations: For a = _f aigi and B = ZET =n bigi ER[G], i=n atB = > ( ai + bi)gi i=1 and 1 =n aB = Ck Jk, 6=1 where ck = _gigi=grab;. If I is an ideal of R show that I[G] is an ideal of R[G], where i=n I[G] = {a = > aigi : ai ED }. i=1