Consider the maximum score estimator with objective functions (S_{N}(beta)) given in (14.29) and (Q_{N}(beta)) given in (14.30). (a) Show that (S_{N}(beta)=Sigma_{i}left[1left(y_{i}=1 ight) times mathbf{1}left(mathbf{x}_{i}^{prime} beta>0

Consider the maximum score estimator with objective functions \(S_{N}(\beta)\) given in (14.29) and \(Q_{N}(\beta)\) given in (14.30).

(a) Show that \(S_{N}(\beta)=\Sigma_{i}\left[1\left(y_{i}=1\right) \times \mathbf{1}\left(\mathbf{x}_{i}^{\prime} \beta>0\right)+\mathbf{1}\left(y_{i}=0\right) \times \mathbf{1}\left(\mathbf{x}_{i}^{\prime} \beta \leq 0\right)\right]\).

(b) Show that \(Q_{N}(\beta)=\Sigma_{i}\left[1\left(y_{i}=1\right) \times \mathbf{1}\left(\mathbf{x}_{i}^{\prime} \beta \leq 0\right)+\mathbf{1}\left(y_{i}=0\right) \times \mathbf{1}\left(\mathbf{x}_{i}^{\prime} \beta>0\right)\right]\).

(c) Using \(\mathbf{1}\left(y_{i}=1\right)=1-1\left(y_{i}=0\right)\), show that \(Q_{N}(\beta)=N-S_{N}(\beta)\).

(d) Using \(\mathbf{1}\left(\mathbf{x}_{i}^{\prime} \boldsymbol{\beta} \leq 0\right)=1-1\left(\mathbf{x}_{i}^{\prime} \boldsymbol{\beta}>0\right)\) show that (14.29) can be rewritten as \(S_{N}(\beta)=\Sigma_{i}\left(2 y_{i}-1\right) 1\left(\mathbf{x}_{i}^{\prime} \beta>0\right)+N-\Sigma_{i} y_{i}\).

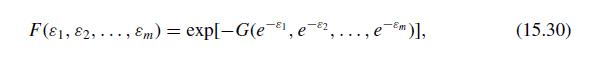
F(1, 2, Em) = exp[-G(e1, e-82 m)1, (15.30)