Consider the multinomial version of the PCGF test given in (8.23) with (p_{j}) replaced by (widehat{p}_{j}=N^{-1} sum_{i} F_{j}left(mathbf{x}_{i}, widehat{boldsymbol{theta}} ight)). Show that PCGF can be

Consider the multinomial version of the PCGF test given in (8.23) with \(p_{j}\) replaced by \(\widehat{p}_{j}=N^{-1} \sum_{i} F_{j}\left(\mathbf{x}_{i}, \widehat{\boldsymbol{\theta}}\right)\). Show that PCGF can be expressed as CGF in (8.27) with \(\widehat{\mathbf{V}}=\operatorname{Diag}\left[N \hat{p}_{i}\right]\). [Conclude that in the multinomial case Andrew's test statistic simplifies to Pearson's statistic.]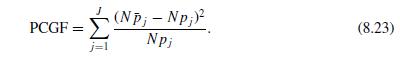

PCGF = (NP; - Np;) j=1 Npj (8.23)