Using the information in the Application "Botox and Price Discrimination," determine how much Allergan loses by being a single-price monopoly rather than a perfectly price-discriminating monopoly. Explain your answer.

Data From Botox and Price Discrimination:-

To show how perfect price discrimination differs from competition and single-price monopoly, we revisit the Application “Botox Patent Monopoly” . The graph shows our estimated linear demand curve for Botox and a constant marginal cost (and average variable cost) of \($25\) per vial. If the market had been competitive (so that price equals marginal cost at ec), consumer surplus would have been triangle A + B + C = \($750\) million per year, and producer surplus and deadweight loss would be zero. In the single-price monopoly optimum, es, the firm sells one million Botox vials at \($400\) each. The corresponding consumer surplus is triangle A = \($187.5\) million per year, producer surplus is rectangle B = \($375\) million, and the deadweight loss is triangle C = \($187.5\) million.

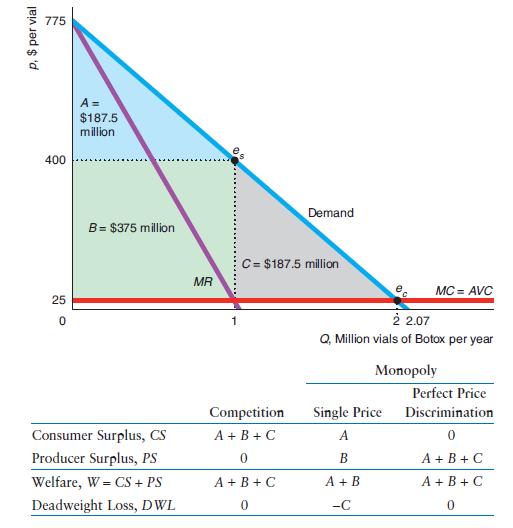
If Allergan, the manufacturer of Botox, could perfectly price discriminate, its producer surplus would double to A + B + C = \($750\) million per year, and consumers would obtain no consumer surplus. The marginal consumer would pay the marginal cost of \($25,\) the same as in a competitive market.
Allergan’s inability to perfectly price discriminate costs the company and society dearly. The profit of the single-price monopoly, B = \($375\) million per year, is lower than what it could earn if it could use perfect price discrimination, A + B + C = \($750\) million per year. Society’s welfare under single-price monopoly is lower than from perfect price discrimination by the deadweight loss, C, of \($187.5\) million per year. However, consumers have no surplus with perfect price discrimination.

Data From Botox Patent Monoply:-

Ophthalmologist Dr. Alan Scott turned the deadly poison botulinum toxin into a miracle drug to treat two eye conditions: strabismus, a condition in which the eyes are not properly aligned, and blepharospasm, an uncontrollable closure of the eyes. Strabismus affects about 4% of children and blepharospasm left about 25,000 Americans functionally blind before Scott’s discovery. His patented drug, Botox, is sold by Allergan, Inc.
Dr. Scott has been amused to see several of the unintended beneficiaries of his research at the annual Academy Awards. Even before it was explicitly approved for cosmetic use, many doctors were injecting Botox into the facial muscles of actors, models, and others to smooth out their wrinkles. (The drug paralyzes the muscles, so those injected with it also lose their ability to frown or smile—and, some would say, act.) The treatment is only temporary, lasting up to 120 days, so repeated injections are necessary.
Allergan has a near-monopoly in the treatment of wrinkles, although plastic surgery and collagen, Restylane, hyaluronic acids, and other filler injections provide limited competition. However, 54% of Botox sales are now for other uses, including as a treatment for chronic migraine and overactive bladder.
Allergan had Botox sales of \($800\) million in 2004 and about \($2.8\) billion in 2015.
Indeed, Botox’s value may increase. As Allergan finds new uses for Botox, its sales continue to increase. According to one forecast, Botox’s global sales will reach \($3\) billion by the end of 2018.
Dr. Scott can produce a vial of Botox in his lab for about \($25.\) Allergan sells the potion to doctors for about \($400.\) Assuming that the firm is setting its price to maximize its short-run profit, we can rearrange Equation 11.9 to determine the elasticity of demand for Botox:

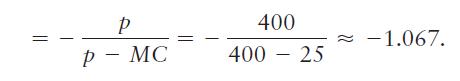
Thus, the demand that Allergan faces is only slightly elastic: A 1% increase in price causes quantity to fall by slightly more than 1%.
If we assume that the demand curve is linear and given that the elasticity of demand is -1.067 at the monopoly optimum, em (1 million vials sold at \($400\) each, producing revenue of \($400\) million in 2002), then Allergan’s inverse demand function was²⁴

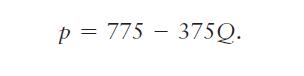
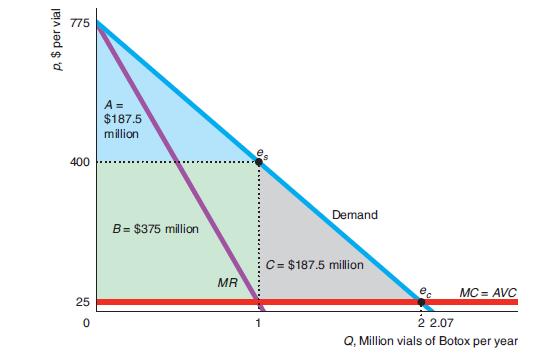This demand curve (see the graph) has a slope of -375 and hits the price axis at \($775\) and the quantity axis at about 2.07 million vials per year. The corresponding marginal revenue curve,

strikes the price axis at \($775\) and has twice the slope, -750, of the demand curve.
The intersection of the marginal revenue and marginal cost curves,

determines the monopoly optimum at the profit-maximizing quantity of 1 million vials per year and at a price of \($400\) per vial.
Were the company to sell Botox at a price equal to its marginal cost of \($25\) (as a competitive industry would), consumer surplus would equal area A + B + C The height of triangle A + B + C is \($750\) = \($775\) - \($25,\) and its length is 2 million vials, so its area is \($750\) (= 12 * 750 * 2) million. At the higher monopoly price of \($400,\) the consumer surplus is A = \($187.5\) million. Compared to the competitive solution, ec, buyers lose consumer surplus of B + C = \($562.5\) million per year. Part of this loss, B = \($375\) million per year, is transferred from consumers to Allergan. The rest, C = \($187.5\) million per year, is the deadweight loss from monopoly pricing. Allergan’s profit is its producer surplus, B, minus its fixed costs.

Transcribed Image Text:

p. $ per vial 400 775 A = $187.5 million B = $375 million Demand MR C = $187.5 million MC=AVC 0 2 25 1 Competition Single Price Consumer Surplus, CS A+B+C A 22.07 Q, Million vials of Botox per year Monopoly Perfect Price Discrimination 0 Producer Surplus, PS 0 B A+B+C Welfare, WCS + PS A+B+C A+ B A+B+C Deadweight Loss, DWL 0 -C 0