(a) Consider H₂O in contact with a heat and volume bath with temperature T and pressure P. For certain values of T and P the H₂O will be liquid water; for others, ice; for others, water vapor—and for certain values it may be a two- or three-phase mixture of water, ice, and/or vapor. Show, using the Gibbs potential and its Euler equation, that, if two phases a and b are present and in equilibrium with each other, then their chemical potentials must be equal: μ_a = μ_b. Explain why, for any phase a, μ_a is a unique function of T and P. Explain why the condition μ_a = μ_b for two phases to be present implies that the two-phase regions of the T -P plane are lines and the three-phase regions are points (see Fig. 5.6). The three-phase region is called the “triple point.” The volume V of the two- or three phase system will vary, depending on how much of each phase is present, since the density of each phase (at fixed T and P) is different.

b. Show that the slope of the ice-water interface curve in Fig. 5.6 (the “melting curve”) is given by the Clausius-Clapeyron equation

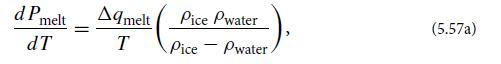
where ρ is density (mass per unit volume), and △q_melt is the latent heat per unit mass for melting (or freezing)—the amount of heat required to melt a unit mass of ice, or the amount released when a unit mass of water freezes. Notice that, because ice is less dense than water, the slope of the melting curve is negative.

(c) Suppose that a small amount of water is put into a closed container of much larger volume than the water. Initially there is vacuum above the water’s surface, but as time passes some of the liquid water evaporates to establish vapor-water equilibrium. The vapor pressure will vary with temperature in accord with the Clausius-Clapeyron equation.

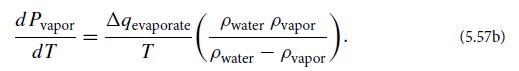
Now suppose that a foreign gas (not water vapor) is slowly injected into the container. Assume that this gas does not dissolve in the liquid water. Show that, as the pressure P_gas of the foreign gas gradually increases, it does not squeeze water vapor into the water, but rather it induces more water to vaporize:

where P_total = P_vapor + P_gas

Figure 5.6

Transcribed Image Text:

dPm melt dT = Aqmelt T Pice Pwater Pice Pwater. - (5.57a)