(a) Derive the equation i = B ij j for the precession angular velocity of a gyroscope at the tip of

(a) Derive the equation △Ω_i = B_ijξ^j for the precession angular velocity of a gyroscope at the tip of ξ as measured in an inertial frame at its tail. Here B_ij is the frame-drag field introduced in Box 25.2.

(b) Show that in linearized theory, B is the symmetrized gradient of the angular velocity Ω_prec of precession of a gyroscope relative to distant inertial frames.

Box 25.2.

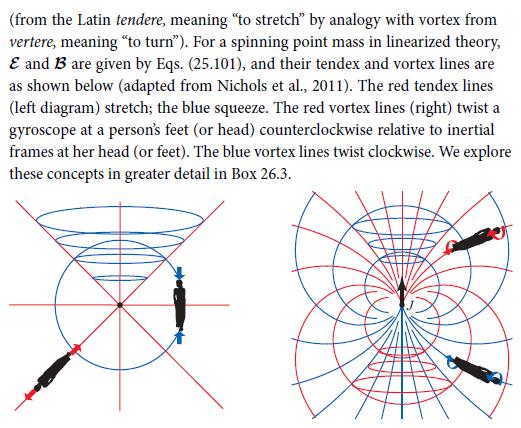
BOX 25.2. DECOMPOSITION OF RIEMANN: TIDAL AND FRAME-DRAG FIELDS T2 In any local Lorentz frame, and also in a Lorentz frame of the linearized theory, the electromagnetic field tensor Fu can be decomposed into two spatial vector fields: the electric field E = Fio and magnetic field Bi=ipg FP9 (Sec. 2.11). Similarly, in vacuum (for simplicity) the Riemann curvature tensor can be decomposed into two spatial tensor fields: the tidal field Ej = Riojo and the frame-drag field Bij =ipg Rajo. The symmetries (25.45) of Riemann, and the fact that in vacuum it is trace-free, imply that both &, and Bjk are symmetric and trace-free (STF). In the 3-space of the chosen frame, they are the irreducible tensorial parts of the vacuum Riemann tensor (cf. Box 11.2). In a local Lorentz frame for strong gravity, and also in the linearized theory for weak gravity, the Bianchi identities (25.70) take on the following Maxwell- like form [Nichols et al., 2011, Eqs. (2.4), (2.15)], in which the superscript S means to symmetrize: V.E=0, V.B=0, a at (V x B) = 0, aB at +(V x E) $ = 0. (1) This has motivated some physicists to call the tidal field & and the frame-drag field B the "electric" and "magnetic" parts of the vacuum Riemann tensor. We avoid this language because of the possibility of confusing these second- rank tensorial gravitational fields with their truly electromagnetic vector-field counterparts E and B.