(a) Write down the explicit form of the Langevin equation for the x component of velocity v(t) of a dust particle interacting with thermalized air molecules.

(b) Suppose that the dust particle has velocity v at time t. By integrating the Langevin equation, show that its velocity at time t + △t is v + △v, where

with R the frictional resistance and m the particle’s mass. Take an ensemble average of this and use F̅’ = 0 to conclude that the function A(v) appearing in the Fokker-Planck equation (6.94) has the form

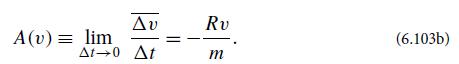
Compare this expression with the first of Eqs. (6.101) to conclude that the mean and relaxation time are v̅ = 0 and τ_r = m/R, respectively, in agreement with the second of Eqs. (6.53a) in the limit τ →∞and with Eq. (6.78).

(c) From Eq. (6.103a) show that

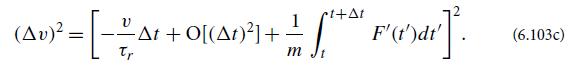
Take an ensemble average of this expression, and use

with the Wiener-Khintchine theorem—to evaluate the terms involving F' in terms of S_F', which in turn is known from the fluctuation-dissipation theorem. Thereby obtain

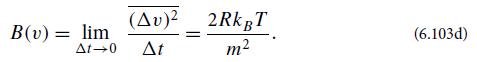
Combine with Eq. (6.101) and τ_r = m/R [from part (b)], to conclude that σ_v²= k_BT/m, in accord with the last of Eqs. (6.53a).

Equations

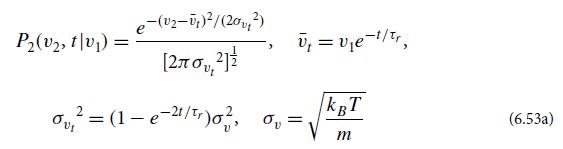
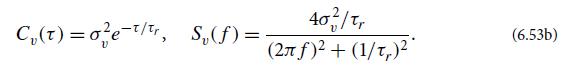
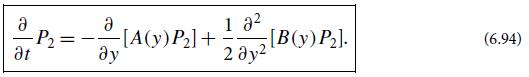
mAv + RvAt +O[(At)] = ct+At F'(t')dt', (6.103a)