Question: Derive Eqs. (6.96) for A and B from the Fokker-Planck equation (6.94), and then from Eqs. (6.96) derive Eqs. (6.97). Equations - P2 t =
Derive Eqs. (6.96) for A and B from the Fokker-Planck equation (6.94), and then from Eqs. (6.96) derive Eqs. (6.97).
Equations
![- P2 t = -[A(y)Pz] + 1 02 2 2 -[B(y) P2].](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2023/04/644e400f21507_806644e400eb13cd.jpg)
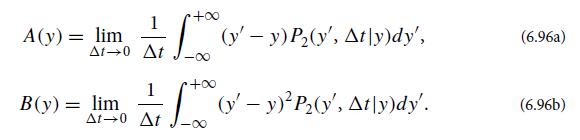
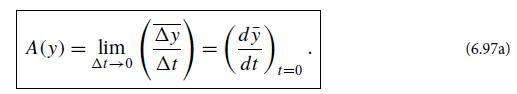
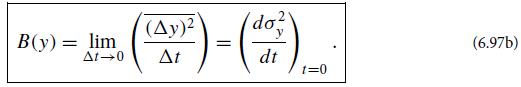
- P2 t = -[A(y)Pz] + 1 02 2 2 -[B(y) P2]. (6.94)
Step by Step Solution
3.44 Rating (167 Votes )
There are 3 Steps involved in it
To derive Eqs 696 from the FokkerPlanck equation 694 we start by considering the FokkerPlanck equation Pt AxPx 2BxPx2 We want to derive the expressions for A and B in terms of the drift and diffusion coefficients as given in Eqs 696 Lets start with A Pt AxPx 2BxPx2 Multiply through by x and integrate over all x xPtdx xAxPxdx x2BxPx2dx Using integration by parts on the second term xPtdx AxPxxdx 2BxPdx BxPxdx The first term on the righthand side can be simplified using the product rule AxPxxdx AxPdx AxPxxdx Now we have xPtdx AxPdx AxPxxdx 2BxPdx BxPxdx Rearranging and combining terms xPt AxPdx AxPx 2BxP BxPxxdx Since the integrals must be equal for all x we can conclude that the integrands are equal xPt AxP AxPx 2BxP BxPx This equation must hold for all x so the coefficients in front of each term must be equal Pt AxPx 2BxP BxPx which gives us Eq 696a Now lets derive Eq 696b for B From the FokkerPlanck equation Pt AxPx 2BxPx2 Multiply through by x2 and integrate over all x x2Ptdx x2AxPxdx x22BxPx2dx Using integration by parts twice on the second term x2Ptdx x2AxPxdx x22BxPx2dx Applying integration by parts to the second term twice we have x2Ptdx AxPxx2dx 2xBxPx 2BxPdx 2BxPx2x2dx The first term on the righthand side can be simplified using the product rule AxPxx2dx AxPx2dx 2xAxPxxdx Now we have x2Ptdx AxPx2dx 2xAxPxxdx 2xBxPx 2BxPdx 2BxPx2x2dx Rearranging and combining terms x2Pt AxPx2dx 2xAxPx 2xBxPx 2BxP 2BxPx2x2dx Again since the integrals must be equal for all x we can conclude that the integrands are equal x2Pt AxPx2 2xAxPx 2xBxPx 2BxP 2BxPx2x2 This equation must hold for all x so the coefficients in front of each term must be equal Pt 2AxPxx 2BxPx2x2 2BxPxx2 AxPx2 Simplifying further Pt 2AxPxx 2BxPx2x2 2BxPxx2 AxPx2 Multiplying through by x2 x2Pt 2xAxPx 2BxPx2 2BxPx AxP Now we compare this equation with the definition of Ax and Bx in Eq 696 Ax 2AxPxx Bx 2BxPx2 2BxPxx2 We can see that the equations for Ax and Bx match the terms on the righthand side of the equation above Therefore we can rewrite the equation as x2Pt xAxP x2BxP AxP Cancelling out the x terms x2Pt xAxP x2BxP AxP Dividing through by x2 Pt AxP BxP AxPx2 Rearranging the terms we obtain Pt BxP AxP1x2 This gives us Eq 697a Finally to derive Eq 697b we substitute the expression ... View full answer

Get step-by-step solutions from verified subject matter experts


