Question: Another magnetic confinement device which brings out some important principles is the spheromak. Spheromaks can be made in the laboratory (Bellan, 2000) and have also
Another magnetic confinement device which brings out some important principles is the spheromak. Spheromaks can be made in the laboratory (Bellan, 2000) and have also been proposed as the basis of a fusion reactor. It is simplest to consider a spheromak in the limit when the plasma pressure is ignorable (low β) and the magnetic field distribution is force-free (Ex. 19.7). We just describe the simplest example of this regime.
(a) As in the previous exercise, assume that α is constant everywhere and, without loss of generality, set it equal to unity. Show that the magnetic field—and also the current density and vector potential, adopting the Coulomb gauge—satisfy the vector Helmholtz equation: ∇2B + α2B = 0.
(b) Introduce a scalar χ such that B = αr × ∇χ + ∇ × (r ×∇χ), with r the radial vector pointing out of the spheromak’s center, and show that χ satisfies the scalar Helmholtz equation: ∇2χ + α2χ = 0.
(c) The Helmholtz equation in part (b) separates in spherical coordinates (r , θ , ∅). Show that it has a nonsingular solution χ = jl(αr)Ylm(θ , ∅), where jl(αr) is a spherical Bessel function, and Ylm(θ , ∅) is a spherical harmonic. Evaluate this for the simplest example, the spheromak, with l = 2 and m = 0.
(d) Calculate expressions for the associated magnetic field in part (c) and either sketch or plot it.
(e) Show that the magnetic field’s radial component vanishes on the surface of a sphere of radius equal to the first zero of jl. Hence explain why a spheromak may be confined in a conducting sphere or, alternatively, by a current-free field that is uniform at large distance.
Data from Exercises 19.7
In an equilibrium state of a very low-β plasma, the plasma’s pressure force density −∇P is ignorably small, and so the Lorentz force density j × B must vanish [Eq. (19.10)]. Such a plasma is said to be “force-free.” As a result, the current density is parallel to the magnetic field, so ∇ × B = αB. Show that α must be constant along a field line, and that if the field lines eventually travel everywhere, then α must be constant everywhere.
Equation 19.10.
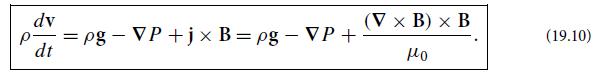
dv p=pg - VP+jx B=pg - VP+ dt (V x B) x B (19.10)
Step by Step Solution
3.37 Rating (163 Votes )
There are 3 Steps involved in it
a In the limit of low plasma pressure ignorable and forcefree magnetic ... View full answer

Get step-by-step solutions from verified subject matter experts


