Around a Schwarzschild black hole, spherical symmetry dictates that every geodesic orbit lies in a plane that

Question:

Around a Schwarzschild black hole, spherical symmetry dictates that every geodesic orbit lies in a plane that bifurcates the t = const 3-volume. We are free to orient our coordinate system, for any chosen geodesic, so its orbital plane is equatorial: θ = π/2. Then the geodesic has three conserved quantities: the orbiting particle’s rest mass μ, energy-at-infinity ε_∞, and angular momentum L, which are given by

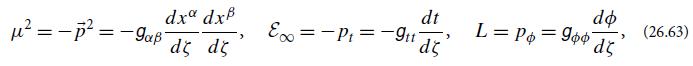
respectively. In this exercise we focus on particles with finite rest mass. Zero-rest-mass particles can be analyzed similarly; see the references at the end of this exercise.

(a) Set the rest mass μ to unity; equivalently, switch from 4-momentumto 4-velocity for the geodesic’s tangent vector. Then, by algebraic manipulation of the constants of motion (26.63), derive the following orbital equations:

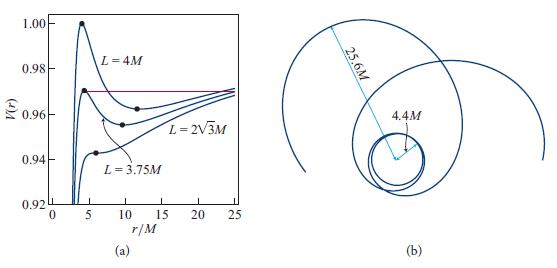
(b) We use a device that we have also encountered in our treatment of ion acoustic solitons in Sec. 23.6. We think of Eq. (26.64a) as an equivalent nonrelativistic energy equation with 1/2V² being the effective potential energy and 1/2ε²_∞ the effective total energy. As the energy we actually care about is ε_∞, it is more direct to refer to V(r) as our potential and investigate its properties. This V(r) is plotted in Fig. 26.7a for several values of the particle’s angular momentum L. Explain why:

(i) Circular geodesic orbits are at extrema of V(r)—the large dots in the figure.

(ii) Each bound orbit can be described by a horizontal line, such as the red one in the figure, with height equal to the orbit’s ε_∞; and the particle’s radial motion is back and forth between the points at which the horizontal line intersects the potential.

(c) Show that the innermost stable circular orbit (often abbreviated as ISCO) is at r = 6M, and it occurs at a saddle point of the potential, for L = 2√3M. Show that all inward-moving particles with L black hole.

(d) Show that the innermost unstable circular orbit is at r = 3M and has infinite energy for finite rest mass. From this infer that there should be an unstable circular orbit for photons at r = 3M.

(e) The geodesic equations of motion in the form(26.64) are not very suitable for numerical integration: at each radial turning point, where V(r) = ε_∞ and dr/dζ = 0, the accuracy of straightforward integrations goes bad, and one must switch signs of dr/dζ by hand, unless one is sophisticated. For these reasons and others, it is preferable in numerical integrations to use the super-hamiltonian form of the geodesic equation (Ex. 25.7), or to convert Eq. (26.64a) into a second-order differential equation before integrating. Show that Hamilton’s equations, for the super-hamiltonian, are

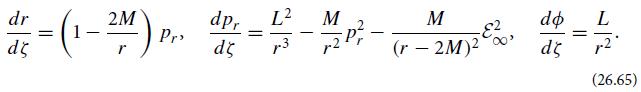
When integrating these equations, one must make sure that the initial value of p_r satisfies g^αβp_αp_β = −1(for our unit-rest-mass particle). Show that this condition reduces to

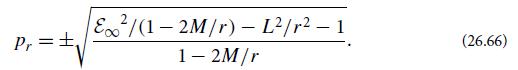
(f) Integrate the super-hamiltonian equations (26.65) numerically for the orbit described by the red horizontal line in Fig. 26.7a, which has L = 3.75M and ε_∞ = 0.9704. The result should be the zoom-whirl orbit depicted in Fig. 26.7b.
(The initial conditions used in that figure were r = 25M, ∅ = 0, and [from Eq. (26.66)] p_r = 0.0339604.)

(g) Carry out other numerical integrations to explore the variety of shapes of finite-rest- mass orbits around a Schwarzschild black hole.

Figure 26.7.

Data from Exercises 26.7.

The equation of state of a neutron star is very hard to calculate at the supra-nuclear densities required, because the calculation is a complex, many-body problem and the particle interactions are poorly understood and poorly measured. Observations of neutron stars’ masses and radii can therefore provide valuable constraints on fundamental nuclear physics. As we discuss briefly in the following chapter, various candidate equations of state can already be excluded on these observational grounds. A necessary step for comparing observation with theory is to compute the stellar structure for candidate equations of state. We can illustrate the approach using a simple functional form, which, around nuclear density (ρ_nuc ≈ 2.3 × 10¹⁷ kgm⁻³), is a fair approximation to some of the models:

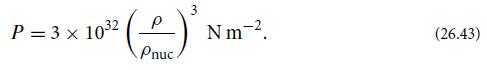
For this equation of state, use the equations of stellar structure (26.38a) and (26.38c) to find the masses and radii of stars with a range of central pressures, and hence deduce a mass-radius relation, M(R).You should discover that, as the central pressure is increased, the mass passes through a maximum, while the radius continues to decrease. (Stars with radii smaller than that at the maximum mass are unstable to radial perturbations.)

Equation (26.38a, 26.38c)