Consider the surface of a zero-pressure star, which implodes along a time like geodesic r = R(t) in the Schwarzschild spacetime of its exterior. Analyze that implosion using Schwarzschild coordinates {t , r, θ, ∅} and the exterior metric (26.1) in those coordinates, and then repeat your analysis in Eddington-Finkelstein coordinates. More specifically, do the following.

(a) Using Schwarzschild coordinates, show that the covariant time component u_t of the 4-velocity u(vector) of a particle on the star’s surface is conserved along its world line (cf. Ex. 25.4a). Evaluate this conserved quantity in terms of the star’s mass M and the radius r = R_o at which it begins to implode.

(b) Use the normalization of the 4-velocity to show that the star’s radius R as a function of the proper time τ since implosion began (proper time as measured on its surface) satisfies the differential equation

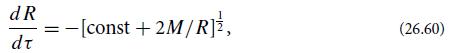
and evaluate the constant. Compare this with the equation of motion for the surface as predicted by Newtonian gravity, with proper time τ replaced by Newtonian time. (It is a coincidence that the two equations are identical.)

(c) Show from the equation of motion (26.60) that the star implodes through the gravitational radius R = 2M and onward to R = 0 in a finite proper time given by Eq. (26.51). Show that this proper time has the magnitudes cited in Eq. (26.51) and the sentences following it.

(d) Show that the Schwarzschild coordinate time t required for the star to reach its gravitational radius, R → 2M, is infinite.

(e) Show, further, that when studied in Eddington-Finkelstein coordinates, the surface’s implosion to R = 2M requires only finite coordinate time t̃; in fact, a time of the same order of magnitude as the proper time (26.51).

(f) Show that the world line of the star’s surface as depicted in an Eddington- Finkelstein spacetime diagram has the form shown in Fig. 26.5a, and that in a Schwarzschild spacetime diagram it has the form shown in Fig. 26.5b.

Data from Exercises 25.4a.

(a) Suppose that in some coordinate system the metric coefficients are independent of some specific coordinate x^A: g_αβ,A = 0 (e.g., in spherical polar coordinates {t , r , θ , ∅} in flat spacetime g_αβ,∅ = 0, so we could set x^A = ∅). Show that

is a constant of the motion for a freely moving particle [p_∅ = (conserved z component of angular momentum)in the above, spherically symmetric example].

Note the analogy of the constant of the motion p_A with Hamiltonian mechanics: there, if the hamiltonian is independent of x^A, then the generalized momentum p_A is conserved; here, if the metric coefficients are independent of x^A, then the covariant component p_A of the momentum is conserved. For an elucidation of the connection between these two conservation laws.

Equations.

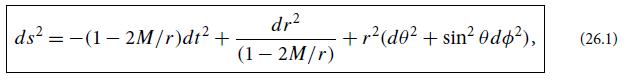
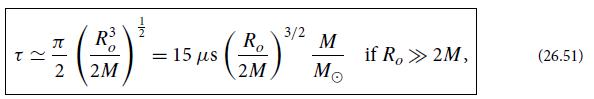
Figure 26.5.

dR dt = - [const+2M/R] , (26.60)