As mountaineers know, it gets cooler as you climb. However, the rate at which the temperature falls
Question:
As mountaineers know, it gets cooler as you climb. However, the rate at which the temperature falls with altitude depends on the thermal properties of air. Consider two limiting cases.
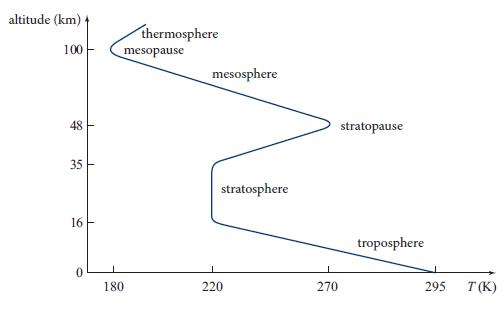
(a) In the lower stratosphere (Fig. 13.2), the air is isothermal. Use the equation of hydrostatic equilibrium (13.4) to show that the pressure decreases exponentially with height z:

where the scale height H is given by

with μ the mean molecular weight of air and mp the proton mass. Evaluate this numerically for the lower stratosphere, and compare with the stratosphere’s thickness. By how much does P drop between the bottom and top of the isothermal region?
(b) Suppose that the air is isentropic, so that P ∝ ργ [Eq. (5) of Box 13.2], where γ is the specific heat ratio. (For diatomic gases like nitrogen and oxygen, γ ∼ 1.4; see Ex. 17.1.) Show that the temperature gradient satisfies
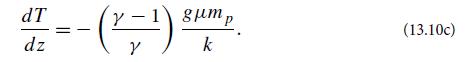
Note that the temperature gradient vanishes when γ →1. Evaluate the temperature gradient, also known at low altitudes as the lapse rate. The average lapse rate is measured to be ∼6 K km−1 (Fig. 13.2). Show that this is intermediate between the two limiting cases of isentropic and isothermal lapse rates.
Equation 5 box 13.2
![]()
Equation 13.4
![]()
Figure 13.2
Data from Exercises 17.1.
Consider an ideal gas consisting of several different particle species (e.g., diatomic oxygen molecules and nitrogen molecules in the case of Earth’s atmosphere).Consider a sample of this gas with volume V, containing NA particles of various species A, all in thermodynamic equilibrium at a temperature T sufficiently low that we can ignore the effects of special relativity. Let species A have νA internal degrees of freedom with the hamiltonian quadratic in their generalized coordinates (e.g., rotation and vibration), and assume that those degrees of freedom are sufficiently thermally excited to have reached energy equipartition. Then the equipartition theorem dictates that each such particle has 3/2kBT of translational energy plus 1/2νAkBT of internal energy, and because the gas is ideal, each particle contributes kBT/V to the pressure. Correspondingly, the sample’s total energy E and pressure P are
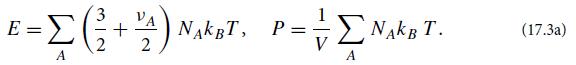
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





