At time t = 0, a 2-dimensional barotropic flowhas a velocity field, in circular polar coordinates, v = (j/)e (Fig. 14.1b); correspondingly, its vorticity

At time t = 0, a 2-dimensional barotropic flowhas a velocity field, in circular polar coordinates, v = (j/ω̅)e_∅ (Fig. 14.1b); correspondingly, its vorticity is ω = 2πjδ(x)δ(y)e_z: it is a delta-function vortex. In this exercise you will solve for the full details of the subsequent evolution of the flow.

(a) Solve the vorticity evolution equation (14.6) to determine the vorticity as a function of time. From your solution, show that the area in which the vorticity is concentrated (the cross sectional area of the vortex) at time t is A ∼ νt, and show that the vorticity is becoming smoothed out—it is evolving toward a state of uniform vorticity, where the viscosity will no longer have any influence.

(b) From your computed vorticity in part (a), plus circular symmetry, compute the velocity field as a function of time.

(c) From the Navier-Stokes equation (or equally well, from Crocco’s theorem), compute the evolution of the pressure distribution P(ω̅, t).

Equation 14.6.

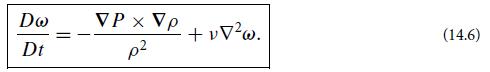
Figure 14.1. b

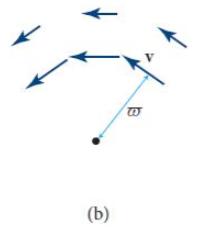
Dw Dt VP x Vp p +vVw. (14.6)