By using more accurate approximations to Eq. (4.48a), explore the onset of the condensation near T = T_c⁰ . More specifically, do the following.
(a) Approximate the numerator in Eq. (4.48a) by q² + 3q, and keep the 1/N₀ term in the exponential. Thereby obtain

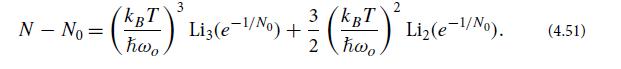
Here

is a special function called the polylogarithm (Lewin, 1981), which is known to Mathematica and other symbolic manipulation software and has the properties

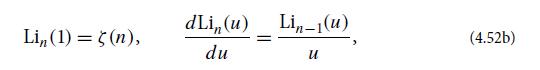
where ζ(n) is the Riemann zeta function.

(b) Show that by setting e^−1/N₀ = 1 and ignoring the second polylogarithm in Eq. (4.51), one obtains the leading-order description of the condensation discussed in the text: Eqs. (4.48b) and (4.49).

(c) By continuing to set e^−1/N₀ = 1 but keeping the second polylogarithm, obtain an improved equation for N₀(T ). Your answer should continue to show a discontinuous turn on of the condensation, but at a more accurate, slightly lower critical temperature

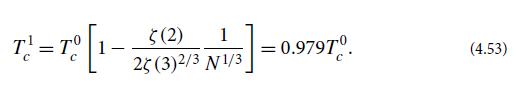
This equation illustrates the fact that our approximations are a large-N expansion (i.e., an expansion in powers of 1/N).

(d) By keeping all details of Eq. (4.51) but rewriting it in terms of T_c⁰, show that

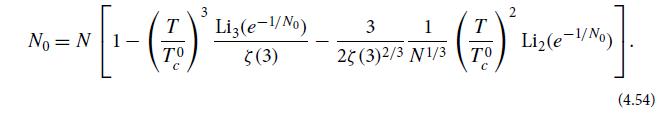
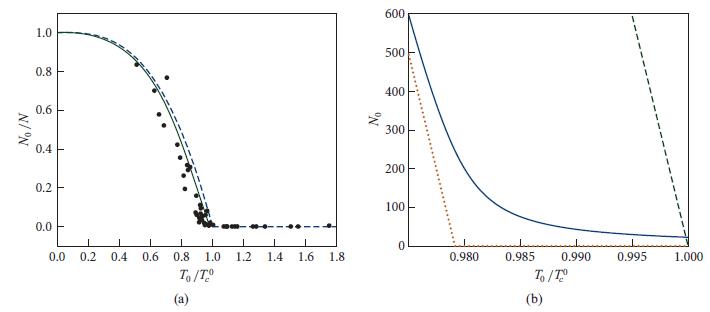
Solve this numerically to obtain N₀(T /T₀^c) for N = 40,000, and plot your result graphically. It should take the form of the solid curves in Fig. 4.4: a continuous turn on of the condensation over the narrow temperature range
In the limit of an arbitrarily large number of atoms, the turn on is instantaneous, as described by Eq. (4.49a)—an instantaneous phase transition.

Fig 4.4

Equation 4.48b and 4.49.

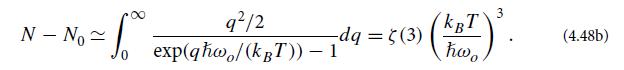
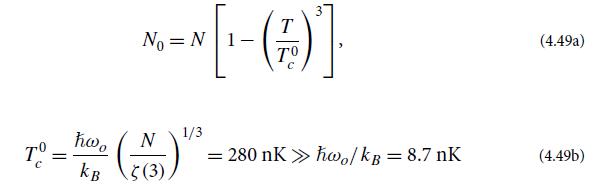
N - No = KBT wo 3 Li3(e-1/No) + 3 (KBT - 2 Li(e-1/No). (4.51)