Consider a 1-dimensionalwave packet with dispersion relation = (k). For concreteness, let A(k)be a narrow Gaussian peaked around (a) Expand as (k) =

Consider a 1-dimensionalwave packet

with dispersion relation ω = Ω(k). For concreteness, let A(k)be a narrow Gaussian peaked around

(a) Expand α as α(k) = α_o − x_oκ with x_o a constant, and assume for simplicity that higher order terms are negligible. Similarly, expand ω ≡ Ω(k) to quadratic order and explain why the coefficients are related to the group velocity V_g at k = k_o by Ω = ω_o + V_gκ + (dV_g/dk)κ²/2.

(b) Show that the wave packet is given by

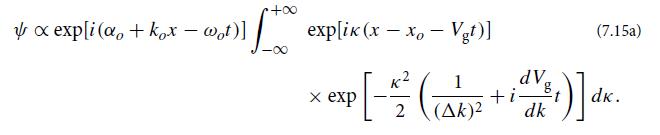(c) Evaluate the integral analytically. From your answer, show that the modulus of ψ satisfies

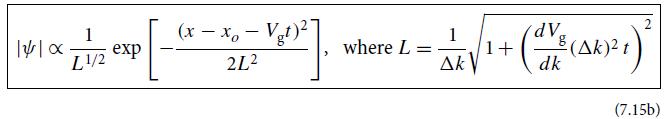
is the packet’s half-width.

(d) Discuss the relationship of this result at time t = 0 to the uncertainty principle for the localization of the packet’s quanta.

(e) Equation (7.15b) shows that the wave packet spreads (i.e., disperses) due to its containing a range of group velocities [Eq. (7.11)]. How long does it take for the packet to enlarge by a factor 2? For what range of initial half-widths can a water wave on the ocean spread by less than a factor 2 while traveling from Hawaii to California?

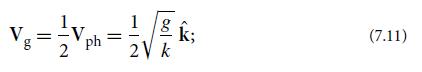
(x, t) = f A(k) ela(k) ei (kx-wt) dk/(2),