Consider the nonrelativistic Schrödinger equation for a particle moving in a time dependent, 3-dimensional potential well:

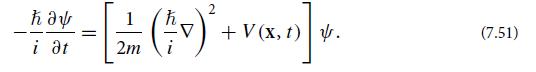
(a) Seek a geometric-optics solution to this equation with the form ψ = Ae^iS/ℏ, where A and V are assumed to vary on a length scale L and timescale T long compared to those, 1/k and 1/ω, on which S varies. Show that the leading order terms in the two-length scale expansion of the Schrödinger equation give the Hamilton-Jacobi equation

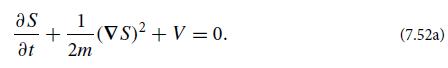
Our notation φ ≡ S/ℏ for the phase φ of the wave function ψ is motivated by the fact that the geometric-optics limit of quantum mechanics is classical mechanics, and the function S = ℏφ becomes, in that limit, “Hamilton’s principal function,” which obeys the Hamilton-Jacobi equation.(b) From Eq. (7.52a) derive the equation of motion for the rays (which of course is identical to the equation of motion for a wave packet and therefore is also the equation of motion for a classical particle):

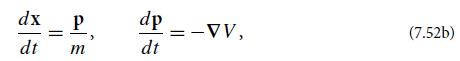
where p = ∇S.

(c) Derive the propagation equation for the wave amplitude A and show that it implies

Interpret this equation quantum mechanically.

ay i t 2 = - [2 / (+/V) * + V (X.) 2m + V (x, t) . V (7.51)