Consider a plane, monochromatic electromagnetic wave with angular frequency , whose electric field is expressed in terms of its complex amplitude X 1 + iX

Consider a plane, monochromatic electromagnetic wave with angular frequency ω, whose electric field is expressed in terms of its complex amplitude X₁ + iX by Eq. (10.58). Because the field (inevitably) is noisy, its quadrature amplitudes X₁ and X₂ are random processes with means X̅₁, X̅₂ and variances △X₁, △X₂.

(a) Normal, classical light has equal amounts of noise in its two quadratures. Explain why it can be represented by Fig. 10.14a.

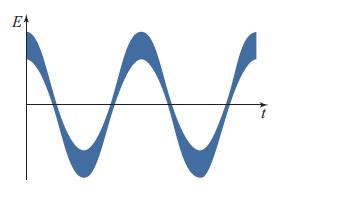
(b) Explain why Fig. 10.14b represents phase-squeezed light, and show that its electric field as a function of time has the form shown in Fig. 10.15.

(c) Explain why Fig. 10.14c represents amplitude-squeezed light, and construct a diagram of its electric field as a function of time analogous to Fig. 10.15.

(d) Figure 10.14d represents the vacuum state of light’s frequency-ω plane-wave mode. Give a formula for the diameter of the mode’s circular error box. Construct a diagram of the electric field as a function of time analogous to Fig. 10.15.

(e) Figure 10.14e represents the squeezed vacuum. Construct a diagram of its electric field as a function of time analogous to Fig. 10.15.

Eq. (10.58).

Fig. 10.14

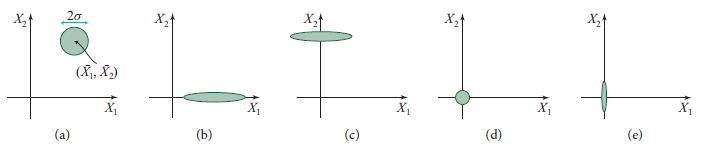
Fig. 10.15

E x R(Ae (ksz@st)) = X cos(kz wst) + X sin(kz - wst). - (10.58)