Consider an ideal fluid interacting with a (possibly dynamical) gravitational field that the fluid itself generates via 2 = 4G. For this fluid,

Consider an ideal fluid interacting with a (possibly dynamical) gravitational field that the fluid itself generates via ∇²Φ = 4πGρ. For this fluid, take the law of energy conservation, ∂U/∂t + ∇ · F = 0, and from it subtract the scalar product of v with the law of momentum conservation, v . [∂(ρv)/∂t + ∇ · T)]; then simplify using the law of mass conservation and the first law of thermodynamics, to obtain ρds/dt = 0. In your computation, use for U and F the expressions given in Eqs. (3) and (4) of Box 13.4. This calculation tells us two things. 

(i) The law of energy conservation for an ideal fluid reduces simply to conservation of entropy moving with the fluid; we have put no dissipative physics into the fluxes of momentum and energy, so we get no dissipation out. 

(ii) The gravitational energy density and flux contained in Eqs. (3) and (4) of Box 13.4 must be correct, since they guarantee that gravity does not alter this “no dissipation in, no dissipation out” result.

Eqs. (3) and (4) of Box 13.4

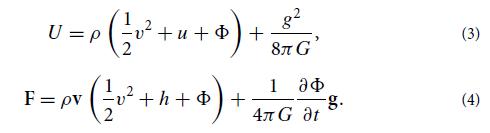
g2 p;+2+u++)+ KG' 1 U=P = A(12+n++) + +h -$) F = pv 4 G at -.. (3) (4)