Consider an inviscid ( = 0), incompressible flow near a plane wall where a laminar boundary layer is established. Introduce coordinates x parallel to the

Consider an inviscid (ν = 0), incompressible flow near a plane wall where a laminar boundary layer is established. Introduce coordinates x parallel to the wall and y perpendicular to it. Let the components of the equilibrium velocity be v_x(y).

(a) Show that a weak propagating-wave perturbation in the velocity, δv_y ∝ exp ik(x − Ct), with k real and frequency Ck possibly complex, satisfies the differential equation

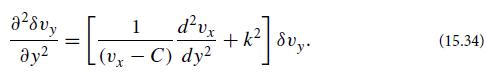
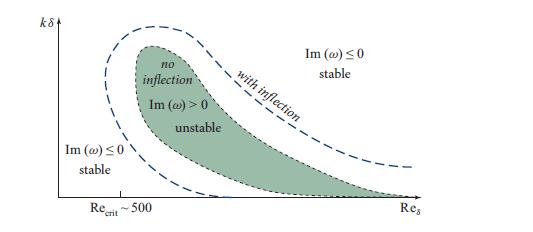
These are called Tollmien-Schlichting waves.(b) Hence argue that a sufficient condition for unstable wave modes [Im(C) > 0] is that the velocity field possess a point of inflection (i.e., a point where d²v_x/dy² changes sign; cf. Fig. 15.12). The boundary layer can also be unstable in the absence of a point of inflection, but viscosity must then trigger the instability.

 Fig. 15.12.

advy y2 1 = [TV = L (vx - C) dy = +k dvy. (15.34)