Question: Consider an optically thick hydrogen gas in statistical equilibrium at temperature T. (Optically thick means that photons can travel only a small distance compared to
Consider an optically thick hydrogen gas in statistical equilibrium at temperature T. (“Optically thick” means that photons can travel only a small distance compared to the size of the system before being absorbed, so they are confined by the hydrogen and kept in statistical equilibrium with it.) Among the reactions that are in statistical equilibrium are H + γ ↔ e + p (ionization and recombination of H, with the H in its ground state) and e + p ↔ e + p + γ (emission and absorption of photons by “bremsstrahlung,” i.e., by the Coulomb-force-induced acceleration of electrons as they fly past protons). Let μ̃γ , μ̃H, μ̃e, and μ̃p be the chemical potentials including rest masses; let mH, me, and mp be the rest masses; denote by I (≡13.6 eV) the ionization energy of H, so that mHc2 = mec2 + mpc2 − I ; denote μj ≡ μ̃j − mjc2; and assume that T≪ mec2/kB ≈ 6 × 109 K and that the density is low enough that the electrons, protons, and H atoms can be regarded as nondegenerate (i.e., as distinguishable, classical particles).
(a) What relationships hold between the chemical potentials μ̃γ , μ̃H, μ̃e, and μ̃p?
(b) What are the number densities nH, ne, and np expressed in terms of T , μ̃H, μ̃e, and μ̃p—taking account of the fact that the electron and proton both have spin 1/2 , and including for H all possible electron and nuclear spin states?
(c) Derive the Saha equation for ionization equilibrium:
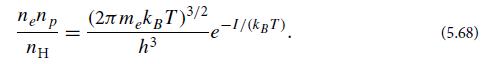
nen p nH = (2 mk T)/-1/(kgT) h3 (5.68)
Step by Step Solution
3.42 Rating (158 Votes )
There are 3 Steps involved in it
a In statistical equilibrium the chemical potentials of all species in the system a... View full answer

Get step-by-step solutions from verified subject matter experts


