Derive the energy-density, energy-flux, and lagrangian properties of elastodynamic waves given in Sec. 12.2.5. Specifically, do the
Question:
Derive the energy-density, energy-flux, and lagrangian properties of elastodynamic waves given in Sec. 12.2.5. Specifically, do the following.
(a) For ease of calculation (and for greater generality), consider an elastodynamic wave in a possibly anisotropic medium, for which
![]()
with Yij kl the tensorial modulus of elasticity, which is symmetric under interchange
(i) Of the first two indices ij
(ii) Of the last two indices kl
(iii) Of the first pair ij with the last pair kl [Eq. (11.17) and associated discussion]. Show that for an isotropic medium
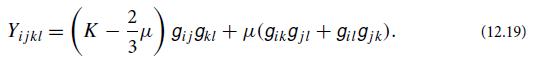
(Recall that in the orthonormal bases to which we have confined ourselves, the components of the metric are gij = δij , i.e., the Kronecker delta.)
(b) For these waves the elastic energy density is 1/2Yij klξi;jξk;l [Eq. (11.25)]. Show that the kinetic energy density minus the elastic energy density,

is a lagrangian density for the waves; that is, show that the vanishing of its variational derivative
![]()
is equivalent to the elastodynamic equations
(c) The waves’ energy density and flux can be constructed by the vector-wave analog of the canonical procedure of Eq. (7.36c):
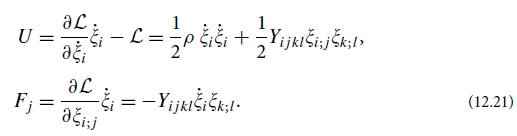
Verify that these density and flux values satisfy the energy conservation law, ∂U/∂t + ∇ · F = 0. Using Eq. (12.19), verify that for an isotropic medium, expressions (12.21) for the energy density and flux become the expressions (12.15) given in the text.
(d) Show that in general (for an arbitrary mixture of wave modes), the time average of the total kinetic energy in some huge volume is equal to that of the total elastic energy. Show further that for an individual longitudinal or transverse, planar, monochromatic mode, the time-averaged kinetic energy density and time-averaged elastic energy density are both independent of spatial location. Combining these results, infer that for a single mode, the time-averaged kinetic and elastic energy densities are equal, and therefore the time-averaged total energy density is equal to twice the time-averaged kinetic energy density. Show that this total time-averaged energy density is given by the first of Eqs. (12.16) and (12.17).
(e) Show that the time average of the energy flux (12.15b) for the longitudinal and transverse modes is given by the second of Eqs. (12.16) and (12.17), so the energy propagates with the same speed and direction as the waves themselves.
Equations
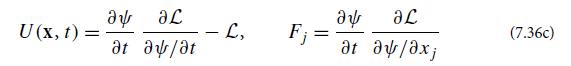

![]()
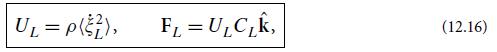
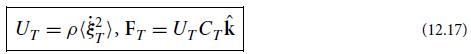
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





