In 3-dimensional Euclidean space Maxwells equation E = e / 0 can be combined with Gausss theorem to show that the electric

In 3-dimensional Euclidean space Maxwell’s equation ∇ · E = ρ_e/∈₀ can be combined with Gauss’s theorem to show that the electric flux through the surface ∂V of a sphere is equal to the charge in the sphere’s interior V divided by ∈₀:

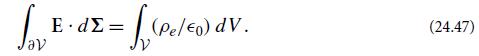
Introduce spherical polar coordinates so the sphere’s surface is at some radius r = R. Consider a surface element on the sphere’s surface with vectorial legs d∅∂/∂∅ and dθ∂/∂θ. Evaluate the components d∑_j of the surface integration element d∑ = ∈(. . . , dθ∂/∂θ , d∅∂/∂∅). (Here ∈ is the Levi-Civita tensor.) Similarly, evaluate dV in terms of vectorial legs in the sphere’s interior. Then use these results for d∑_j and dV to convert Eq. (24.47) into an explicit form in terms of integrals over r, θ, and ∅. The final answer should be obvious, but the above steps in deriving it are informative.

dav Ed = (pe/eo) dV. (24.47)