This exercise serves two roles: It develops the relativistic stress-energy tensor for a viscous fluid with diffusive heat conduction, and in the process it allows the reader to gain practice in index gymnastics.

In our study of elasticity theory, we introduced the concept of the irreducible tensorial parts of a second-rank tensor in Euclidean space (Box 11.2). Consider a relativistic fluid flowing through spacetime with a 4-velocity (vector)u(P).The fluid’s gradient ∇(vector)u(vector) (u_α;β in slot-naming index notation) is a second-rank tensor in spacetime. With the aid of the 4-velocity itself, we can break it down into irreducible tensorial parts as follows:

Here: 

(i)

is a tensor that projects vectors into the 3-space orthogonal to u(vector). 

(ii) σ_αβ is symmetric, trace-free, and orthogonal to the 4-velocity; 

(iii) ω_αβ is antisymmetric and orthogonal to the 4-velocity.

(a) Show that the rate of change of u(vector) along itself, ∇_u(vector)u(vector) (i.e., the fluid 4-acceleration) is equal to the vector a(vector) that appears in the decomposition (24.52). Show, further, that a(vector) · u(vector) = 0.

(b) Show that the divergence of the 4-velocity, ∇ · u(vector), is equal to the scalar field θ that appears in the decomposition (24.52). As we shall see in part (d), this is the fluid’s rate of expansion.

(c) The quantities σ_αβ and ω_αβ are the relativistic versions of a Newtonian fluid’s shear and rotation tensors, which we introduced in Sec. 13.7.1. Derive equations for these tensors in terms of u_α;β and P_μν.

(d) Show that, as viewed in a Lorentz reference frame where the fluid is moving with speed small compared to the speed of light, to first order in the fluid’s ordinary velocity v^j = dx^j/dt , the following statements are true:

(i) u⁰ = 1, u^j = v^j ; 

(ii) θ is the nonrelativistic rate of expansion of the fluid, θ = ∇ · v ≡ v^j, _j [Eq. (13.67a)];

(iii) σ_jk is the fluid’s nonrelativistic shear [Eq. (13.67b)]; 

(iv) ω_jk is the fluid’s nonrelativistic rotation tensor [denoted r_ij in Eq. (13.67c)].

(e) At some event P where we want to know the influence of viscosity on the fluid’s stress-energy tensor, introduce the fluid’s local rest frame. Explain why, in that frame, the only contributions of viscosity to the components of the stress-energy tensor are

where ζ and μ are the coefficients of bulk and shear viscosity, respectively; the contributions to T⁰⁰ and T^j0 = T^0j vanish.

(f) From nonrelativistic fluid mechanics, infer that, in the fluid’s rest frame at P, the only contributions of diffusive heat conductivity to the stress-energy tensor are

where κ is the fluid’s thermal conductivity and T is its temperature.

Actually, this expression is not fully correct. If the fluid is accelerating, there is a correction term: ∂T /∂x^j gets replaced by ∂T /∂x^j + a^jT , where a^j is the acceleration. After reading Sec. 24.5 and especially Ex. 24.16, explain this correction.

(g) Using the results of parts (e) and (f), deduce the following geometric, frame in variant form of the fluid’s stress-energy tensor:

Here the subscript parentheses in the last term mean to symmetrize in the α and β slots.

Equation 13.67.

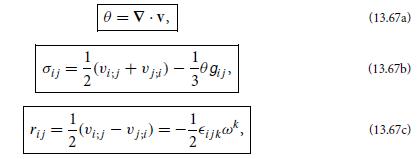
Ex. 24.16.

Inside a laboratory on Earth’s surface the effects of spacetime curvature are so small that current technology cannot measure them. Therefore, experiments performed in the laboratory can be analyzed using special relativity. 

(a) Explain why the space time metric in the proper reference frame of the laboratory’s floor has the form

plus terms due to the slow rotation of the laboratory walls, which we neglect in this exercise. Here g is the acceleration of gravity measured on the floor.

(b) An electromagnetic wave is emitted fromthe floor, where it is measured to have wavelength λ_o, and is received at the ceiling. Using the metric (24.75), show that, as measured in the proper reference frame of an observer on the ceiling, the received wave has wavelength λ_r = λ_o(1+ gh), where h is the height of the ceiling above the floor (i.e., the light is gravitationally redshifted by △λ/λ_o = gh).

The first high-precision experiments to test this prediction were by Robert Pound and his student Glen Rebka and postdoc Joseph Snider, in a tower at Harvard University in the 1950s and 1960s. They achieved 1% accuracy. We discuss this gravitational redshift in Sec. 27.2.1.

Box 11.2.

Transcribed Image Text:

Μα;β —aquB + 50 Ραβ 3 == + σαβ + Θαβ· (24.52)