In astrophysics (e.g., in supernova explosions and in jets emerging from the vicinities of black holes), one
Question:
In astrophysics (e.g., in supernova explosions and in jets emerging from the vicinities of black holes), one sometimes encounters shock fronts for which the flow speeds relative to the shock approach the speed of light, and the internal energy density is comparable to the fluid’s rest-mass density.
(a) Show that the relativistic Rankine-Hugoniot equations for such a shock take the following form:
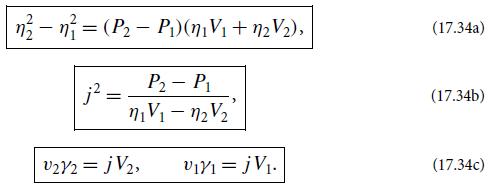
Here,
(i) We use units in which the speed of light is 1.
(ii) The volume per unit rest mass is V ≡ 1/ρo, and ρo is the rest-mass density (equal to some standard rest mass per baryon times the number density of baryons; cf. Sec. 2.12.3).
(iii)We denote the total density of mass-energy including rest mass by ρR and the internal energy per unit rest mass by u, so ρR = ρo(1 + u). In terms of these the quantity η ≡ (ρR + P)/ρo = 1+ u + P/ρo = 1 + h is the relativistic enthalpy per unit rest mass (i.e., the enthalpy per unit rest mass, including the rest-mass contribution to the energy) as measured in the fluid rest frame.
(iv) The pressure as measured in the fluid rest frame is P.
(v) The flow velocity in the shock’s rest frame is v, and
![]()
(not the adiabatic index!), so vγ is the spatial part of the flow 4-velocity.
(vi) The rest-mass flux is j (rest mass per unit area per unit time) entering and leaving the shock.
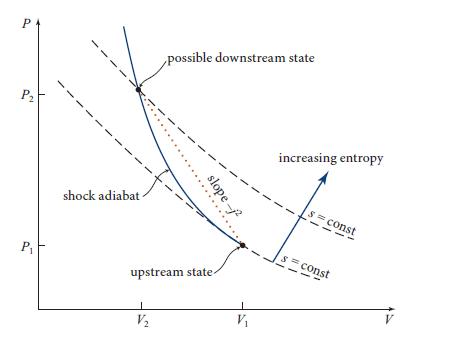
(b) Use a pressure-volume diagram to discuss these relativistic Rankine-Hugoniot equations in a manner analogous to Fig. 17.11.
(c) Show that in the nonrelativistic limit, the relativistic Rankine-Hugoniot equations (17.34) reduce to the nonrelativistic ones (17.31).
(d) It can be shown (Thorne, 1973) that relativistically, just as for nonrelativistic shocks, in general P2 > P1, V2 1, and v2 1. Consider, as an example, a relativistic shock propagating through a fluid in which the mass density due to radiation greatly exceeds that due to matter (a radiation-dominated fluid), so P = ρR/3 (Sec. 3.5.5). Show that v1v2 = 1/3, which implies v1 > 1/√3 and v2 2/P1 = (9v12 − 1)/[3(1− v12)].
Figure 17.11.
Equation 17.31.
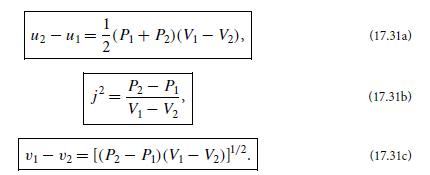
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





