In the film Fultz (1969), about 20 min 40 s into the film, an experiment is described in which Rossby waves are excited in a rotating cylindrical tank with inner and outer vertical walls and a sloping bottom. Figure 16.10a is a photograph of the tank from the side, showing its bottom, which slopes upward toward the center, and a hump on the bottom that generates the Rossby waves. The tank is filled with water, then set into rotation with an angular velocity Ω. The water is given time to settle down into rigid rotation with the cylinder. Then the cylinder’s angular velocity is reduced by a small amount, so the water is rotating at angular velocity △Ω≪ Ω relative to the cylinder. As the water passes over the hump on the tank bottom, the hump generates Rossby waves. Those waves are made visible by injecting dye at a fixed radius through a syringe attached to the tank. Figure 16.10b is a photograph of the dye trace as seen looking down on the tank from above. If there were no Rossby waves present, the trace would be circular. The Rossby waves make it pentagonal. In this exercise you will work out the details of the Rossby waves, explore their physics, and explain the shape of the trace.

Because the slope of the bottom is cylindrical rather than planar, this is somewhat different from the situation discussed in the text (see Fig. 16.9). However, we can deduce the details of the waves in this cylindrical case from those for the planar case by using geometric-optics considerations (Sec. 7.3), making modest errors because the wavelength of the waves is not all that small compared to the circumference of the tank.

(a) Using geometric optics, show that the rays along which the waves propagate are circles centered on the tank’s symmetry axis.

(b) Focus on the ray that is halfway between the inner and outer walls of the tank. Let its radius be a, the depth of the water there be h, and the slope angle of the tank floor be α. Introduce quasi-Cartesian coordinates x = a∅ and y = −ω̅, where {ω̅, ∅, z} are cylindrical coordinates. By translating the Cartesian-coordinate waves of the text into quasi-Cartesian coordinates and noting from Fig. 16.10b that five wavelengths must fit into the circumference around the cylinder, show that the velocity field has the form v_ω̅ , v_∅, v_z ∝ e^i(5∅+ωt), and deduce the ratios of the three components of velocity to one another. The solution has nonzero radial velocity at the walls—a warning that edge effects will modify the waves somewhat. This analysis ignores those edge effects.

(c) Because the waves are generated by the ridge on the bottom of the tank, the wave pattern must remain at rest relative to that ridge, which means it must rotate relative to the fluid’s frame with the angular velocity d∅/dt = −△Ω. From the waves’ dispersion relation, deduce △Ω/Ω (the fractional slowdown of the tank that had to be imposed to generate the observed pentagonal wave).

(d) Compute the displacement field δx(ω̅, ∅, z, t) of a fluid element whose un-displaced location (in the rigidly rotating cylindrical coordinates) is (ω̅, ∅, z). Explain the pentagonal shape of the movie’s dye lines in terms of this displacement field.

(e) Compute the wave’s vertical vorticity field ω_z (relative to the rigidly rotating flow), and show that as a fluid element moves and the vertical vortex line through it shortens or lengthens due to the changing water depth, ω_z changes proportionally to the vortex line’s length.

Figure 16.9

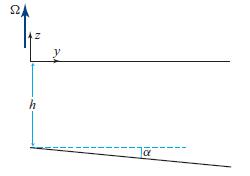
Figure 16.10.

Transcribed Image Text:

42 h α