The moment generating function G(t) is defined by

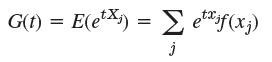
or

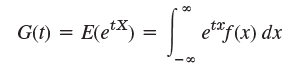
where X is a discrete or continuous random variable, respectively.

(a) Assuming that term wise differentiation and differentiation under the integral sign are permissible, show that E(X^k) = G^(k)(0), where G^(k) = d^kG/dt^k, in particular, μ = G'(0).

(b) Prove (4).

(c) Show that the Poisson distribution has the moment generating function G(t) = e^-μe^μet and prove (6).

(d) 

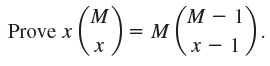
Using this, prove (9).

G-Ee)-f) G(t) = E(e*X) etaf(x) dx