Question: Show that the matrices (2.37a), with and satisfying Eq. (2.37b), are the inverses of each other, and that they obey the condition (2.35b)

Show that the matrices (2.37a), with β and γ satisfying Eq. (2.37b), are the inverses of each other, and that they obey the condition (2.35b) for a Lorentz transformation.

[2] - 0 0 Y 0 1 0 1 Y - -

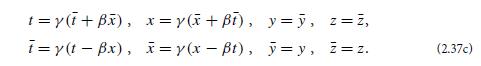
[2] - 0 0 Y 0 1 0 1 Y - - Y > 0 0 10 0 001 (2.37a)

Step by Step Solution

★★★★★

3.36 Rating (162 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To show that the matrices 237a are inverses of each other we need to multiply them an... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Classical Physics Questions!

In a half-wave rectifier, the load current flows for more than half cycle but less than complete cycle of the input signal O less than half cycle of the input signal O either positive half cycle or...

chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS The purpose of this chapter is to introduce you to matrix algebra, which has many applications. You are already familiar with several algebras:...

The eigenfunctions Î± and Î² of the Hermitian operator S^z form a complete, orthonormal set, and any one-electron spin function can be written as c1Î± +...

Please help with the following matrices questions: *Appreciate it if you can show your work If you are unable to view the questions below, here is link https://massey.limfinity.com/207/hillcipher.pdf...

Note: Summarize the article in your own wording with a professional format. MACROECONOMIC VARIABLES AND STOCK MARKETS: AN INTERNATIONAL STUDY Francisco JAREO Ana ESCRIBANO Alberto CUENCA Abstract....

I need help in doing these in MAT LAB Question1 Use Matrices in MATLAB to solve the following system of linear equations 2z30 5x + 12y - 2x Question 2 Use the following matrix to answer the questions...

Need to do this in MATLAB Question 1 Use Matrices in MATLAB to solve the following system of linear equations. -4x + 3y + z = -18 5x + 12y-2z = 30 2a- Question2 Use the following matrix to answer the...

using MATLAB 29. Create the following three matrices: 1-35 10-21 A- 2 2 4 B = 5 1 -6 C- 08 2 -2 06 (2 7 -1 -3 5 3 (a) Calculate A+B and B+A to show that addition of matrices is commuta- tive. (b)...

[Q8] (Section 5.4: The Spectral Theorem) Recall that a matrix A e Cox is called normal if AA* = A*A, where A* is the conjugate transpose of A. If A e R"*", then this condition is AA" = A'A. The class...

solve this matrixes and explain them to me 5. Pauli matrices are defined as 01 = (9 1).62 = (9 7).03 = 10 (a) Show that Pauli matrices are Hermitian, i.e. the conjugate transpose are themselves. (5...

A jet of water having a velocity of 15 m/s strikes a curved vane which is moving with a velocity of 15 m/s. The vane is symmetrical and it so shaped that the jet is deflected through 120. Find the...

Write a paper that uses game theory to set up a game designed to help a consumer decide whether to buy life insurance or not. To keep the game relatively simple, assume the life insurance being...

To qualify as a comparable, a sale must be all of the following except: Group of answer choices a competitive property an open market transaction exactly equal to the subject property recent in time...

It is not necessary to repeat the message or make further reference to the bad news.

FIGURE EX2.7 is a somewhat idealized graph of the velocity of blood in the ascending aorta during one beat of the heart. Approximately how far, in cm, does the blood move during one beat? Figure Ex...

FIGURE EX2.8 shows the velocity graph for a particle having initial position x 0 = 0 m at t 0 = 0 s. At what time or times is the particle found at x = 35 m? Figure Ex 2.8 V (m/s) 10- 5. 0- 2 4 6 -t...

FIGURE EX2.9 shows the velocity graph of a particle. Draw the particles acceleration graph for the interval 0 s ¤ t ¤ 4 s. Figure Ex 2.9 (m/s) 4+ 2- t (s) 0+ 2

1-2 Martinez Companys relevant range of production is 7,500 units to 12,500 units. When it produces and sells 10,000 units, its average costs per unit are as follows: Average Cost per Unit Direct...

XYZ company has a total debt ratio (or just the debt ratio) of 0.37. Please note that as far as this class is considered we total debt ratio and debt ratio refer to the same quantity. What is its...

Help Save & Exit Check my The following is the ending balances of accounts at December 31, 2018 for the Vosburgh Electronics Corporation. Account Title Debits Credits Cash 107,000 Short-term...