Simplify the analysis by treating each Gaussian light beam as though it were a plane wave. The answers for the phase shifts will be the same as for a true Gaussian beam, because on the optic axis, the Gaussian beam’s phase [Eq. (8.40a) with ω̅ = 0] is the same as that of a plane wave, except for the Gouy phase tan⁻¹(z/z₀), which is very slowly changing and thus is irrelevant.

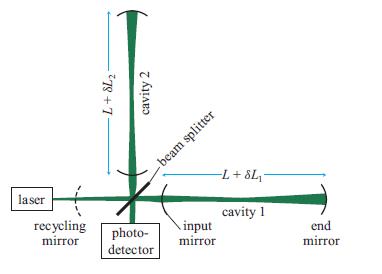
(a) For the interferometric gravitational-wave detector depicted in Fig. 9.13 (with the arms’ input mirrors having amplitude reflectivities r_i close to unity and the end mirrors idealized as perfectly reflecting), analyze the light propagation in cavity 1 by the same techniques as used for an etalon in Sec. 9.4.1. Show that, if ψ_i1 is the light field impinging on the input mirror, then the total reflected light field ψ_r1 is

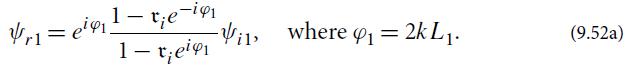
(b) From this, infer that the reflected flux |ψ_r1|² is identical to the cavity’s input flux |ψ_i1|², as it must be, since no light can emerge through the perfectly reflecting end mirror.

(c) The arm cavity is operated on resonance, so φ₁ is an integer multiple of 2π. From Eq. (9.52a) infer that (up to fractional errors of order 1− ri) a change δL₁ in the length of cavity 1 produces a change

With slightly different notation, this is Eq. (9.47), which we used in the text’s order-of-magnitude analysis of LIGO’s sensitivity. 

Eq. (8.40a)

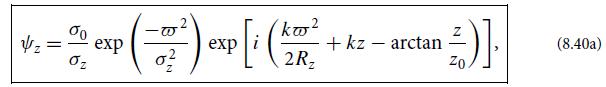
Eq. (9.47)

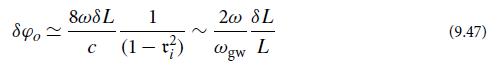
Fig. 9.13

Transcribed Image Text:

Vr₁= eig₁1-t₁e-i9₁ 1 - teigi -V, where ₁ = 2k L₁. 91 (9.52a)