Suppose that some medium has a rest frame(unprimed frame) in which its energy flux and momentum density vanish, T^0j = T^j0 = 0. Suppose that the medium moves in the x direction with speed very small compared to light, v ≪ 1, as seen in a (primed) laboratory frame, and ignore factors of order v².The ratio of the medium’s momentum density G_j´ = T^j´0´ (as measured in the laboratory frame) to its velocity v_i = vδ_ix is called its total inertial mass per unit volume and is denoted ρ_ji^inert:

In other words, ρ_ji^inert is the 3-dimensional tensor that gives the momentum density G_j´ when the medium’s small velocity is put into its second slot.(a) Using a Lorentz transformation from the medium’s (unprimed) rest frame to the (primed) laboratory frame, show that

(b) Give a physical explanation of the contribution T_jiv_i to the momentum density.

(c) Show that for a perfect fluid [Eq. (2.74b)] the inertial mass per unit volume is isotropic and has magnitude ρ + P, where ρ is the mass-energy density, and P is the pressure measured in the fluid’s rest frame:

See Ex. 2.26 for this inertial-mass role of ρ + P in the law of force balance.

Data from Ex. 2.26

Energy-Momentum Conservation for a Perfect Fluid(a) Derive the frame-independent expression (2.74b) for the perfect fluid stress energy tensor from its rest-frame components (2.74a).(b) Explain why the projection of ∇(vector) · T = 0 along the fluid 4-velocity, u(vector) . (∇(vector) · T ) = 0, should represent energy conservation as viewed by the fluid itself. Show that this equation reduces to

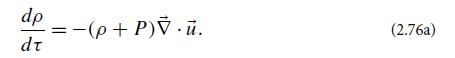
With the aid of Eq. (2.65), bring this into the form

where V is the 3-volume of some small fluid element as measured in the fluid’s local rest frame. What are the physical interpretations of the left- and right-hand sides of this equation, and how is it related to the first law of thermodynamics?

(c) Read the discussion in Ex. 2.10 about the tensor P = g + u(vector) ⊗ u(vector) that projects into the 3-space of the fluid’s rest frame. Explain why P_μαT^αβ_;β = 0 should represent the law of force balance (momentum conservation) as seen by the fluid. Show that this equation reduces to

where a(vector) = du(vector)/dτ is the fluid’s 4-acceleration. This equation is a relativistic version of Newton’s F = ma. Explain the physical meanings of the left- and righthand sides. Infer that ρ + P must be the fluid’s inertial mass per unit volume. It is also the enthalpy per unit volume, including the contribution of rest mass.

Tj'O inert = Pji V. (2.77)