A test function as part of the integrand is required to prove any delta function identity. With this in mind: (a) Prove that (ax) =

A test function as part of the integrand is required to prove any delta function identity. With this in mind:

(a) Prove that δ(ax) = 1/|a|δ(x), a ≠ 0.

(b) Use the identity in part (a) to prove that

(c) Confirm that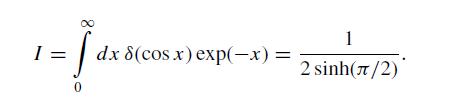

8[g(x)] = [ m 1 [g'(xm)| 8(x - xm), where g(x) = 0 and g'(xm) 0.