Consider time-harmonic solutions to the Maxwell equations in vacuum where the fields are independent of the azimuthal angle . TEM solutions of this type also

Consider time-harmonic solutions to the Maxwell equations in vacuum where the fields are independent of the azimuthal angle φ. TEM solutions of this type also have no radial component to the fields: E_r = B_r = 0.
(a) Show that the conditions stated above decouple the Maxwell curl equations into two subsets, each of which describes a different type of TEM wave.
(b) Begin with the Maxwell divergence equations and find general solutions for E(r, θ, t) and B(r, θ, t) for each of the two TEM wave types.
(c) The figure below shows the apex of an infinite, solid conducting cone touching the conducting half-space z

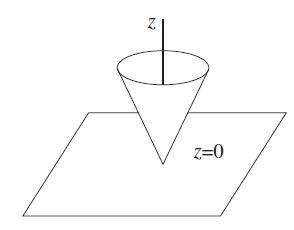
N z=0