Let the half-space z 0 be filled with a magnetic crystal where H = 1 B. The inverse permeability matrix 1

Let the half-space z ≥ 0 be filled with a magnetic crystal where H = μ⁻¹ · B. The inverse permeability matrix μ⁻¹ is (rows and columns labeled by x, y, z)

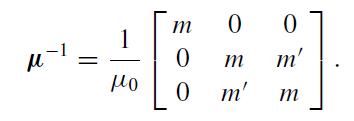
Assume that ε =  ε₀ inside the crystal and that the real, dimensionless matrix elements satisfy m > m' > 0.

(a) Show that ω(k, θ) = ck √m − m' sin 2θ for a wave E = x̂ E₀ exp[i(k · r − ωt)] inside the crystal when k = k(ŷ sin θ + ẑ cos θ).
(b) A plane wave E = x̂E₀ exp[i(kz − ωt)] is incident on this crystal from the vacuum (z

-1 = 1 Mo m 0 0 0 m m' 0 m' m