This problem outlines a contour integration method to prove that

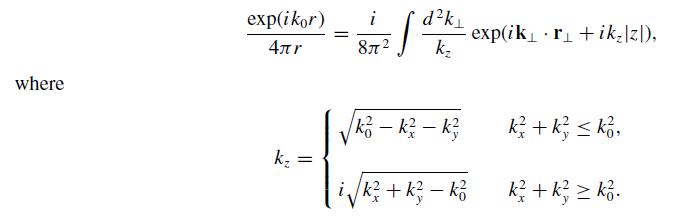
See Problem 8.23 for another method.

(a) The left side of the Weyl identity is the free-space Green function, G₀(r), which satisfies (∇² + k²₀)G₀(r) = −δ(r). Fourier transform this differential equation and show that

(b) Use contour integration to perform the integral over k_z in part (a). Assume that k₀ has a small positive imaginary part to establish the location of the poles and to decide how to close the contour.

Data From Problem 8.23

Write δ(r − r') = δ(r_⊥ − r'_⊥)δ(z − z') and use direct integration to derive Weyl’s formula for the free-space Green function in three dimensions,

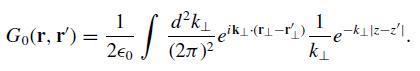
where exp(ikor) i 4r 87 k = = dk k k-k-k ik+k k exp(ikr +ik[z]), k+k k, k+k k.