Question: Without using vector identities: (a) Use Stokes Theorem dS ( A) = ds A with A = c F where

Without using vector identities:
(a) Use Stokes’ Theorem ∫ dS · (∇ ×A) = ∮ ds · A with A = c × F where c is an arbitrary constant vector to establish the equality on the left side of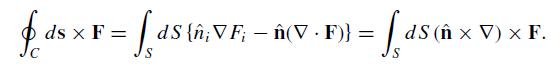 f ds x F = [ dS (, VF, - (V -

(b) Confirm the equality on the right side of this expression.

f ds x F = [ dS (, VF, - (V - F)] = [ds ( ; VF dS ( x V) x F.

Step by Step Solution

★★★★★

3.34 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Let p c F Then because c is a constant vector This shows that cF ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Electrodynamics Questions!

As the water rises on the left side of the rectangular gate, the gate will open automatically. At what depth above the hinge will this occur? Neglect the mass of the gate.

Use Theorem 4.15 show that Theorem 4.15 If X1, X2, . . . , Xn are random variables and Where a1, a2, . . . , an, b1, b2, . . . , bn are constants, then cov(A, B) =--. 2 rt 2 -1 71 (a,b, +a cov(X,X)...

Use the proof of Theorem 8.5 to show that equality in the Cauchy-Schwarz Inequality holds if and only if x = 0, y = 0, or x is parallel to y.

Please only answer ques 5-9 3:27 Reset Done 8. [7 marica] Use Stokes' theorem to compute the surface integral N - / (V xG) . ds for the voctor field G(z, y. 2) = (ever.x3=), where & is the half of...

4. Given the vector field F = x2yzi + yz2j + ze*yk. Use Stokes' Theorem to calculate If curl F . ds. S is the part of the sphere x2 + y2 + z2 = 5 that lies above the plane z=1 and S is oriented...

Give Correct ANSWERS Human-Computer Interaction (a) If you had been one of the original inventors of the WIMP interface, and engineers on the technical team had been sceptical about the advantages...

(5) Let C be the closed curve given by the intersection of the hyperbolic paraboloid z = yr and the cylinder x + y = 1 oriented anticlockwise as viewed from above. Let H be the part of the same...

need help quickly please; will give like for correct solution \fDef. A vector field F is said to be conservative if it is the gradient of some scalar field, i.e., if there exists a scalar field f...

Could you please help me with my homework? Please clearly show and organize your work. Professor has completed 70-90 percent of the work Please, please, please follow his work. 6 8 ( x , y , E ) ds 8...

1 E ) Let C be a closed curve oriented counterclockwise that is a rectangle in two dimensions with vertices ( 0 , 0 ) , ( c + 2 , 0 ) , ( c + 2 , d + 1 ) , and ( 0 , d + 1 ) in the x y - plane. Using...

Modify Figure to focus on open source packages. Purchasing Advantages Reduced time to implement Lower overall acquisition costs Reduced need for internal IS resources High application quality...

From the following adjusted trial balance (ATB) titles on a worksheet, identify in which column each account will be listed in the last four columns of the worksheet. (ID) Income statement, Dr....

( a ) ( 1 0 % ) Find two trapping sets of the ( 1 0 , 6 ) LDPC code from the null space over GF ( 2 ) of H which are different from those given in Fig 1 1 . 1 2 . ( a ) ( 1 0 % ) Find another two...

One of the fust Internet-based groceries home delivery businesses was Homegrocer.com. In 1998, Mike Donald, president of Concord Sales, one of the largest food brokers in B.C., and two partners...

Fractional composition in a triprotic system. For a triprotic system, the fractional composition equations are where D = [H + ] 3 + K 1 [H + ] 2 + K1K 2 [H + ] + K 1 K 2 K 3 . Use these equations to...

Explain what is wrong with the following statement: At its isoelectric point, the charge on all molecules of a particular protein is 0.

Calculate the pH at each of the following points in the titration of 50.00 mL of 0.010 0 M NaOH with 0.100 M HCl. Volume of acid added: 0.00, 1.00, 2.00, 3.00, 4.00, 4.50, 4.90, 4.99, 5.00, 5.01,...

Cooper Technologies Ltdis a company that provides geospatial services for national governments, states, provinces, counties, municipalities, and commercial organisations around the world. The...

In 2018, Caterpillar Inc. had about 650 million shares outstanding. Their book value was $25.0 per share, and the market price was $155.80 per share. The companys balance sheet shows that the company...

Growth Annuities Question 3 (1 point) A payment starts out as $0, but undergoes growth of $6.10 per month for a total lifetime of 28 months. Calculate the equivalent uniform payment amount if the...