Question: A simple massspring system, subject to light damping, is vibrating under the action of a periodic force Fcos pt. The equation of motion is where

A simple mass–spring system, subject to light damping, is vibrating under the action of a periodic force Fcos pt. The equation of motion is

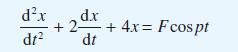
dx dt +2- + 4x = Fcospt d.x dt

where F and p are constants. Solve the differential equation for the displacement x(t). Show that one part of the solution tends to zero as t → ∞ and show that the amplitude of the steady state solution is

Hence show that resonance occurs when p = √2.

dx dt +2- + 4x = Fcospt d.x dt

Step by Step Solution

★★★★★

3.49 Rating (159 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

This is a secondorder linear constantcoefficient nonhomogeneous ordinary differential equation We ca... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Engineering Mathematics Questions!

P1, P2, and P3 are partners in XYZ Inc. Their capital balances on Dec 31, Year 5, are $177,495 for P1. $246529 for P2, and $130,654 for P3. Among these partners on this date, the income sharing...

A three-phase, 339.4-V, ABC system [Fig. 11-15(a)] has a -connected load, with Obtain the phase and line currents and draw the phasor diagram. ZAB = 10/0 2 ZBC = 10/30 2 ZCA 15-30 2

Let Fs = (1,x, x), F = (1+x,1+x,1 + 2x 2x), F' = (1-x, 1-, 1-2x + 2x). Let Ms= - (69) (9) 6 ) C 9)), (G). (1). ( 2) (9) (1 M = 2 M': -(( 2) ( 2) ( 3) ( 3)) 9 For exercises 1 - 4 see Method (5.4.1)....

Using "On the Spectrum of Hydrogen" by Niels Bohr -What is the main idea of the Author's argument? What is the main essence of the piece? -What ways does the author use to propose and support their...

Write down the change equation for this system. Indicate what each term represents and include the units for each term. Exercise C. Consider the mass-spring systeln described on pp. 32-34 in the...

question c and d Question 3 The suspension system in a car (Figure 3) can be modelled by a simple mass-spring system. Each wheel is attached to the car's body by means of an elastic spring. Inside...

The objective of this HW is to use the ode45 command in Matlab to solve the state-space problems we have previously set up. Taken from Matlab Help, the syntax for ode45 is: [T,Y] =...

3. The equation of motion of a general mass-spring system subject to an external force F(t) is mx" + cx' + kx = F(t) where m, c and k are the mass, damping coefficient and spring constant...

Please provide the Matlab code to solve this question, thank you !!! The equation of motion of a general mass-spring system subject to an external force F(t) is mx"(t) + cx'(t) + kx(t) = F(t) where...

This is algebra phiscys. Please answer these learning objectives clearly 1-5 with no calculas use as I would not understand it. O Bco-1 1. Demonstrate an understanding, both conceptually and...

18) The daily cost of operating a hospital, C is a linear function of the number of in-patients, and out- patients P, plus a fixed cost a, where C=a+bP+dl. Given the data in the table below, Days 1 2...

Describe the two types of compliance services that may be performed under AT section 601.

In a valuation model that is based on free cash flow, the proper discount rate is termimal value the required rate of return on the stock No answer text provided. weighted average cost of capital

prepare a set of accounts for an integrated and interlocking cost accounting system;

The structural assembly supports the loading shown. Draw the moment diagrams for each of the beams. Take I = 100(10 6 ) mm 4 for the beams and A = 200 mm 2 for the tie rod. All members are made of...

The contilevered beam is supported at one end by a 1/2 in.-diameter suspender rod AC and fixed at the other end B. Determine the force in the rod due to a uniform loading of 4 k/ft. E = 29(10 3 ) ksi...

The beam AB has a moment of inertia I = 475 in 4 and rests on the smooth supports at its ends. A 0.75-in-diameter rod CD is welded to the center of the beam and to the fixed support at D. If the...

Implement the following socket programming in C (c) Security Protocol(Cryptography Concepts-Encryption@Sender and decryption@ Receiver)

Assume you own 330 shares of a firm with a total of 1,125 shares outstanding. The total value of the firm is currently estimated to be $550,000. A year later the firm sells 390 new shares to a...

Q4 4. Define activation records. Explain how it is related with runtime storage allocation. 5. Generate code for the following C program using any code generation algorithm